Графическое изображение опытного распределения показателя надежности
Составленный по данным исходной информации статистический ряд дает полную характеристику опытного распределения показателя надежности.
По данным статистического ряда могут быть построены гистограмма полигон и кривая накопленных опытных вероятностей , которые дают наглядное представление об опытном распределении показателя надежности и позволяют в первом приближении решать ряд инженерных задач, связанных с оценкой надежности строительных и мелиоративных машин.
Несколько практических рекомендаций по правилам построения графиков опытного распределения и пользования ими.
При выборе масштаба желательно придерживаться правила «золотого сечения»:
![]() ,
,
где Y - длина наибольшей ординаты, а Х - длина абсциссы, соответствующая наибольшему значению показателя надежности.
По оси абсцисс всех графиков откладывают в масштабе значение показателя надежности t, а по оси ординат - частоту или опытную вероятность у гистограммы и полигона и накопленная опытная вероятность у кривой накопленных вероятностей (см. рис. 3, 4 и 5).
Гистограмма является дифференциальным, а кривая накопленных опытных вероятностей - интегральным статистическими (опытными) законами распределения показателей надежности.
Площадь каждого прямоугольника гистограммы или соответствующая этому же интервалу площадь полигона определяет опытную вероятность или количество машин (в долях единицы), у которых значение показателя надежности находится в границах этого интервала.
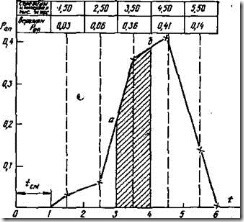
Рис. 4. Полигон распределения доремонтного ресурса двигателя
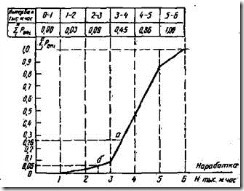
Рис. 5. Кривая накопленных опытных вероятностей
Точки полигона (см. рис. 4) образуются пересечением ординаты, равной опытной вероятности интервала, и абсциссы, равной середине этого интервала. Точки кривой накопленных опытных вероятностей (см. рис. 5) образуются пересечением ординаты, равной сумме вероятностей предыдущих интервалов, и абсциссы конца данного интервала.
Начальная и конечная точки полигона распределения приравниваются к абсциссе начала первого и конца последнего интервалов статистического ряда. Считать количественное значение ординаты за вероятность появления показателя надежности, величина которого равна абсциссе соответствующей точки, является грубой ошибкой, так как в этом случае ширина интервала равна нулю, а следовательно, и вероятность появления показателя надежности в этой точке также равна нулю.
Гистограмма и полигон, представленные на рис. 3 и 4, построены по данным испытания двигателей на доремонтный ресурс (см. табл. 1). Пользуясь этими графиками, можно определить количество двигателей, которые потребуют ремонта в заданном интервале их наработок (например от 3 до 4 тыс. мото-ч). Для этого надо определить площадь полигона или гистограммы, ограниченную заданным интервалом, которая и будет равна в процентах или долях единицы искомому количеству двигателей или числу ремонтов (площадь 3аб4 на рис. 4).
Более удобно решать задачи подобного рода с помощью интегральной кривой, показанной на рис. 5. В этом случае не требуется производить подсчет площадей - все искомые результаты определяются непосредственно по масштабу оси ординат.
Например, требуется определить количество двигателей, которые потребуют ремонта с начала эксплуатации и до их средней наработки Н=3500 мото-ч. Для этого находим ординату точки а (см. рис. 5), равную 0,26, и соответственно определим, что к наработке 3500 мото-ч 26 % (или 18 шт.) двигателей потребуют ремонта.
С помощью интегральной кривой можно рассчитывают количество двигателей, вышедших из строя в интервале наработок, например, от 2500 до 3500 мото-ч. Для этого из ординаты точки а, соответствующей Н=3500 мото-ч, надо вычесть ординату точки d, соответствующую Н=2500 мото-ч. В нашем случае 0,26-0,06=0,20 т.е. 20 % двигателей потребуют ремонта в интервале наработок от 2500 до 3600 мото-ч.


