Машиностроение и механика

Article Index
Основы расчёта надежности мелиоративных и строительных машин
Статистический ряд информации
Абсолютные характеристики рассеивания показателей надежности
Проверка информации на выпадающие точки
Графическое изображение опытного распределения показателя надежности
коэффициент вариации
Теоретические законы распределения показателей надежности
Критерии согласия опытных и теоретических распределений показателей надежности
Укрупненный статистический ряд информации для определения критерия согласия c2
Распределение критерия Колмогорова
Дифференциальная и интегральная функции законов распределения
Закон нормального распределения показателей надежности и его практическое применение
Опытные и теоретические вероятности выхода из строя двигателей
Доверительные границы рассеивания одиночного и среднего значения показателя надежности
Пример расчета доверительных границ одиночного показателя надежности
Абсолютная и относительная предельные ошибки
All Pages

Пример расчета доверительных границ одиночного показателя надежности

Расчет 1.2. В ПМК имеется 12 бульдозеров ДЗ-42, на которых установлены новые двигатели СМД-17. Требуется определять, в каком диапазоне наработок будет производиться ремонт этих двигателей (доверительные границы рассеивания доремонтного ресурса), если известно, что рассеивание доремонтных ресурсов двигателей подчинено закону нормального распределения с параметрами:

мото-ч, s=910 мото-ч.

Доверительной вероятностью задаемся а=0,90.

Порядок расчета.

1) Определим по прил. 2 значение коэффициента t_а для а=0,90 и N=12

t_a=1,80.

2) Определим по уравнениям (32) и (33) доверительные границы наработок до постановки двигателей в ремонт:

мото-ч.

мото-ч.

Доверительный интервал I_а, определим по уравнению (34)

мото-ч.

В случае распределения Вейбулла определение доверительных границ рассеивания одиночного показателя надежности производится по такой же принципиальной схеме, как и при законе нор­мального распределения.

Наиболее характерным и имеющим большое практическое значение примером использования закона распределения Вейбулла является определение доверительных границ остаточного ресурса Т₀ конкретной детали или сопряжения, если известны параметры распределения или хотя бы опытный коэффициент вариации V.

Все сказанное выше относится только к определению доверительных границ одиночного показателя надежности.

В практике чаще приходится встречаться с расчетом доверительных границ среднего значения показателя надежности.

Расчетная схема и физический смысл доверительных границ при заданной доверительной вероятности а для среднего значения показателя надежности остаются такими же, как и для одиночного показателя (см. рис. 11 и 12).

Разница заключена в определении величины среднего квадратического отклонения.

Если представить, что было проведено n испытаний совокупностей из N машин и в каждом случае определялись средние значения показателя надежности , то ясно, что эти средние будут отличаться друг от друга по величине, рассеиваясь вокруг истинного, но неизвестного нам, математического ожидания. Рассеивание средних значений , естественно, будет тем больше, чем меньше число машин N участвовало при каждом испытании. Однако даже при самых малых значениях N среднее квадратическое отклонение этих средних значений будет меньше среднего квадратического отклонения одиночного показателя надежности s. Связь между и s установлена в теории вероятностей:

. (35)

Таким образом, по аналогии с (31)-(34) и с учетом (30) расчётными уравнениями для определения рассеивания среднего значения показателя надежности при законе нормального распределения и заданной доверительной вероятности а являются:

абсолютная ошибка:

; (36)

нижняя доверительная граница:

; (37)

верхняя доверительная граница

; (38)

доверительный интервал

. (39)

Рис. 12. Доверительные границы остаточного ресурса детали или сопряжения при распределении Вейбулла

Расчет 2.2. На основании проведенных испытаний 69 новых двигателей СМД-17 было установлено, что рассеивание их доремонтного ресурса подчинено закону нормального распределения с параметрами мото-ч и s=910 мото-ч.

Спрашивается:

а) если вновь провести испытания таких же 69 двигателей, то в каких пределах может измениться их средний доремонтный ресурс?

б) в хозяйстве одновременно работают 12 новых двигателей СМД-17. При планировании их загрузки в каких пределах сле­дует учитывать возможные изменения величины среднего доремонтного ресурса, если известны результаты испытания 69 двигателей?

Для решения этих задач зададимся доверительной вероятностью а=0,90 и определим коэффициент Стьюдента t_a (прил. 2):

для случая «a» t_a=1,67,

для случая «б» t_a=1,80.

По уравнениям (37) и (38) определим доверительные границы рассеивания доремонтного ресурса двигателя СМД-17:

для случая «а»

мото-ч,

мото-ч;

для случая «б»

мото-ч,

мото-ч,

Как и следовало ожидать, доверительные границы у доремонтного ресурса двигателя СМД-17 во втором случае (случай «б») вследствие меньшего количества машин в хозяйстве (N=12) будут шире, чем при N=69.

Аналогично определяют доверительные границы рассеивания среднего значения показателя надежности при законе Вейбулла.

Приведем без выводов уравнения для определения доверительных границ по Вейбуллу при заданной доверительной вероятности а с учетом и без учета смещения начала рассеивания t_см.

а) С учетом смещения нижняя и верхняя доверительные границы рассеивания показателя надежности определяются по уравнениям:

; (40)

. (41)

б) Без учета смещения доверительные границы определяются по уравнениям:

; (42)

, (43)

где r₁ и r₃ - коэффициенты Вейбулла, определяемые по прил. 2 в зависимости от заданной величины доверительной вероятности а и повторности информации N.

Применительно к основному расчету ( мото-ч, b=3,0, t_см=1500 мото-ч), задавшись доверительной вероятностью а= 0,90, по табл. прил. 3 (для N=69) определим:

r₁=1,18; r₃=0,86.

Доверительные границы среднего доремонтного ресурса будут соответственно равны уравнения (40) и (41):

мото-ч;

мото-ч.

В отличие от закона нормального распределения доверительные границы при распределении Вейбулла асимметричны среднему значению показателя надежности : верхняя граница отличается от среднего значения на большую величину, чем нижняя.

В практике часто приходится определять односторонние доверительные границы: верхнюю или нижнюю. Так, например, в технических условиях на новую или отремонтированную машину (агрегат) указывают, что средний доремонтный (межремонтный) ресурс должен превышать заданный гарантийный ресурс при до верительной вероятности а.

Будем считать, что заданный гарантийный ресурс является нижней доверительной границей среднего ресурса (в этом случае верхняя граница не указывается).

Для решения этой задачи следует считать, что вся площадь за нижней границей равна а, а до нижней границы - соответственно 1-а (при двусторонних доверительных границах слева от нижней и справа от верхней границ располагались площади, равные ).

Таким же образом распределяются площади и при односторонней верхней доверительной границе (правее верхней границы площадь равна 1-а).

На этом основании при определении односторонних доверительных границ следует пользоваться теми же уравнениями, что и при определении двусторонних доверительных границ, только значения коэффициентов t_а, r₃, и r₁ следует брать в прил. 2 на колонку левее. Например, при заданной дове­рительной вероятности а=0,90 значения t_a, r₁ и r₃ надо брать из колонки для а=0,80; при заданной доверительной вероятности а=0,95 значения t_а, r₁ и r₃ следует брать из колонки для а=0,90 и т. д.

Для того чтобы не путать обозначения в дальнейшем при определении односторонних доверительных границ, коэффициенты будут обозначаться: t_0a, r₀₁ и r₀₃.

Расчет 3.2. Определить нижнюю одностороннюю доверительную границу доремонтного ресурса двигателя при законе нормального распределения ( мото-ч, s=910 мото-ч) при доверительной вероятности а=0,90.

По прил. 2 для N=69 определим, что t_0a =1,29 (а не 1,67, как при двусторонних доверительных границах).

По уравнению (37) рассчитаем нижнюю одностороннюю доверительную границу:

мото-ч.

Верхняя односторонняя доверительная граница при а=0,90 будет равна (уравнение 38)

мото-ч.

При переносе результатов испытания машин из одной совокупности в другую или в другие условия эксплуатации может изменяться не только среднее значение показателя надежности, но и опытное значение его среднего квадратического отклонения s.

Двусторонние доверительные границы рассеивания s при заданной доверительной вероятности а для закона нормального распределения определяются по уравнениям:

; (44)

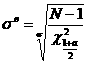; (45)

где c² - коэффициент Пирсона (определяется по прил. 2).

При законе распределения Вейбулла могут быть определены доверительные границы параметров а и b (ГОСТ 17509-72).

<< Prev - Next >>