Определение надежности и технологиявосстановления деталей машин
Основы расчета надежности мелиоративных и строительных машин
Из-за неудовлетворительного качества новых или отремонтированных машин при их эксплуатации, показатели надежности имеют значительные отклонения. Вследствие этого они относятся к категории случайных величин.
Вероятность появления случайной величины в конкретном опыте или в процессе испытания машин называется опытной вероятностью.
Математическую и опытную вероятности определяют по формулам:
![]() ; (1)
; (1)
![]() , (2)
, (2)
где Р(А) и р(А) – соответственно математическая и опытная вероятности появления случайного события (отказа) А; М и m – соответственно расчетное и опытное число появления события А; N – общее число опытов или количество наблюдаемых машин.
Инженерную сущность опытной вероятности можно проиллюстрировать для конкретного предприятия. Возможен расчет расхода деталей на группу машин, например, бульдозеров, скреперов и т. д. Это в значительной степени приведет к экономии времени и средств на проведение ремонтов и приобретение запасных частей в ПМК, ДРСУ и т.п.
Обработка опытной информации по надежности мелиоративных и строительных машин
Сбор информации
Учитывая значительное рассеивание первичной информации, при испытании машин первостепенное значение имеет правильный выбор количества одновременно испытуемых машин (повторность информации).
Недостаточное количество машин при испытании может внести значительную ошибку в результаты расчетов показателей надежности и сделать их непригодными для практического использования. С другой стороны, слишком большая повторность испытаний, хотя и обеспечит высокую точность расчетов, будет неприемлема из экономических соображений вследствие высокой стоимости таких испытаний. Таким образом, необходимо подобрать оптимальное решение, при котором количество испытываемых машин, при достаточной точности конечных результатов, не будет громоздким, а сами испытания не слишком дорогими.
Информация, полученная в процессе испытания (наблюдения) машин, сводится в таблицы, которые являются основой для последующей математической обработки и расчета показателей надежности.
В качестве примера в табл. 1 приведены фактические данные по доремонтным ресурсам 70 однотипных двигателей. Эта информация в дальнейшем будет использована для обработки и расчетов показателей надежности.
Обработка информации
Принципиальные исходные положения, составляющих основу обработки информации по надежности строительных машин, следующие:
Все показатели надежности относятся к категории случайных величин.
Основными характеристиками каждого показателя надежности являются:
- среднее значение (математическое ожидание);
- характеристики рассеивания - среднее квадратическое отклонение s и коэффициент вариации V;
- доверительные границы рассеивания одиночного и среднего значений показателя надежности;
- наибольшие возможные абсолютная и относительная погрешности;
Показатели надежности являются существенными положительными величинами. В связи с этим у многих показателей свойств надежности (доремонтный, межремонтный, полный ресурсы, время восстановления, стоимость восстановления и др.) начало зоны рассеивания может существенно смещаться относительно его нулевого значения. Величину такого смещения tсм следует учитывать при определении коэффициента вариации и подборе теоретического закона распределения показателя свойств надежности.
Общая схема математической обработки опытной информации по показателям надежности и последовательность выполнения отдельных этапов представлены на рис. 1 применительно к информации по доремонтным ресурсам испытуемых двигатей (см. табл. 1);
В нижней части рис. 1 показано количество ресурсных отказов двигателей в течение каждых 1000 мото-часов их работы за весь период испытаний.
Основными этапами обработки информация являются:
составление сводной таблицы исходной информации в порядке возрастания показателя надежности (доремонтного ресурса) - (см. рис. 1);
составление статистического ряда исходной информации - (см. рис. 1);
определение среднего значения и абсолютных характеристик рассеивания (дисперсии и среднеквадратического отклонения) показателя надежности;
проверка информации на выпадающие точки;
графическое изображение опытной информации: построение гистограммы, полигона и кривой накопленных опытных вероятностей показателя надежности - 3, 4, 5 (см. рис. 1);
определение относительного показателя рассеивания показателя надежности - коэффициента вариации;
выбор теоретического закона распределения, определение его параметров и графическое построение дифференциальной и интегральной кривых - 6, 7 (см. рис. 1);
проверка совпадения опытных и теоретических законов распределения показателя надежности по критериям согласия;
определение доверительных границ рассеивания одиночных и средних значений показателя надежности и наибольших возможных ошибок расчета.
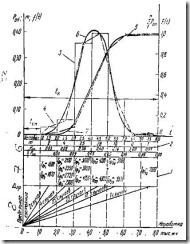
Рис. 1. Схема последовательной обработки информации


