Закон нормального распределения показателей надежности и его практическое применение
Закон нормального распределения (закон Гаусса) широко используется во многих отраслях науки и техники. Применительно к показателям надежности тракторов, сельскохозяйственных машин и их элементов закон нормального распределения (ЗНР) используется в случаях:
определения характеристик рассеивания полных, доремонтных и межремонтных ресурсов машин, их агрегатов и узлов;
определения характеристик рассеивания (времени и стоимости восстановления работоспособности машины и ее элементов;
определения характеристик рассеивания наработок на один ресурсный отказ;
определения характеристик рассеивания ошибок измерения и размеров деталей в пределах допуска;
сложения нескольких одинаковых или разных законов распределения.
Приведенные случаи применения ЗНР не являются обязательными. Иногда рассеивание перечисленных показателей надежности подчинено другим законам распределения. Поэтому в каждом конкретном случае расчета необходимо производить проверку правильности выбора закона распределения.
Закон нормального распределения, как и все другие законы, характеризуется дифференциальной ¦(t) и интегральной F(t) функциями. Отличительной особенностью этих функций является симметричное рассеивание частных значений показателей надежности относительно среднего значения.
Дифференциальная функция (или плотность вероятности нормального распределения) определяется по уравнению:
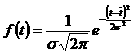, (23)
где е - основание натурального логарифма (е=2,718); p - 3,14; ![clip_image018[6]](/images/stories/clip_image0186_thumb_1.gif "clip_image018[6]"){kind=small}
- среднее значение показателя надежности; s - среднее квадратическое отклонение.
Если в уравнении (23) среднее значение показателя надежности ![clip_image018[7]](/images/stories/clip_image0187_thumb_1.gif "clip_image018[7]"){kind=small}
приравнять нулю, а среднее квадратическое отклонение s - единице, то получим выражение для центрированной дифференциальной функции:
. (24)
Центрированная функция (19) табулирована при условии нормирования показателя надежности в долях среднего квадратического отклонения s. В прил. 2 даны значения центрированной и нормированной дифференциальной функции нормального распределения ¦0(t).
Из уравнений (18) и (19) получим:
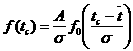. (25)
Следовательно:
, (26)
где tс - среднее значение показателя надежности в заданном интервале А или значение середины интервала статистического ряда; А - величина заданного интервала значений показателя надежности или величина интервала статистического ряда.
При проведении инженерных расчетов характеристик надежности следует пользоваться уравнением (25) и табл. 1 прил. с учетом зависимости (26).
Интегральную функцию или функция распределения F(t) получают интегрированием функции плотности вероятности ¦(t)
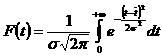. (27)
Центрированная и нормированная интегральная функция (s=1,0 и ![clip_image018[8]](/images/stories/clip_image0188_thumb_1.gif "clip_image018[8]"){kind=small}
=0) определяется уравнением:
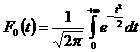. (28)
Центрированная интегральная функция F0(t) табулирована, ее значения приведены в прил. 2.
Из уравнений (27) и (28) получим:
. (29)
где tк - значение заданного показателя надежности или конца интервала статистического рада.
Из уравнения (28) следует, что
. (30)
При расчете характеристик показателей надежности следует пользоваться уравнениями (29) и (30), определяя при этом значение F0(t) по прил. 2.
Покажем применение закона нормального распределения в целях выравнивания опытной информации на примере результатов испытания двигателей на доремонтный ресурс (см. табл. 1).
В результате первичной обработки информации было установлено:
средний доремонтный ресурс Тдр=4100 мото-ч;
среднее квадратическое отклонение s=910 мото-ч;
коэффициент вариации V=0,32.
С учетом величины коэффициента вариации (0,32<0,33) заменяем опытное статистическое распределение функциями закона нормального распределения с параметрами Тдр=4100 мото-ч и s=910 мото-ч.
Для того чтобы убедиться в совпадении статистического и выбранного теоретического законов распределения доремонтного ресурса двигателя, построим теоретические дифференциальную и интегральную кривые и наложим их соответственно на полигон и кривую накопленных опытных вероятностей (см. рис. 1).
Для построения дифференциальной кривой ¦(t) определим теоретическую вероятность или количество двигателей (в долях единицы), которые потребуют ремонта в каждом интервале статистического ряда (см. табл. 4).
Рассчитаем количество двигателей, вышедших из строя в интервале их наработок от 1000 до 2000 мото-ч (середина интервала tс=1500 мото-ч).
Согласно (25) и (26):
.
Определим значение ¦0(2,86) по прил. 2 и 8-я колонка, 2-я строка снизу): ¦0(2,86)=0,007.
Окончательно получим:
¦(1000…2000)=1,10×0,007=0,01,
т.е. 1 % двигателей необходимо ремонтировать в интервале наработок от 1000 до 2000 мото-ч.
Соответственно для интервала от 2000 до 3000 мото-ч (tс=2500 мото-ч):
,
или 9 % двигателей потребуют ремонта в этом интервале наработок.
Для интервала от 3000 до 4000 мото-ч получим:
и т. д.
Расчетные теоретические вероятности для сравнения с опытной вероятностью заносим в табл. 7 по каждому интервалу статистического ряда (4-я строка), а дифференциальную кривую ¦(t) наложим на полигон (рис. 1).
Для построения интегральной кривой F(t) определим значения ординат по концам интервалов статистического ряда. Так, например, для конца 1-го интервала (tк = 2000 мото-ч) согласно (24):
.