Машиностроение и механика

Article Index
Основы расчёта надежности мелиоративных и строительных машин
Статистический ряд информации
Абсолютные характеристики рассеивания показателей надежности
Проверка информации на выпадающие точки
Графическое изображение опытного распределения показателя надежности
коэффициент вариации
Теоретические законы распределения показателей надежности
Критерии согласия опытных и теоретических распределений показателей надежности
Укрупненный статистический ряд информации для определения критерия согласия c2
Распределение критерия Колмогорова
Дифференциальная и интегральная функции законов распределения
Закон нормального распределения показателей надежности и его практическое применение
Опытные и теоретические вероятности выхода из строя двигателей
Доверительные границы рассеивания одиночного и среднего значения показателя надежности
Пример расчета доверительных границ одиночного показателя надежности
Абсолютная и относительная предельные ошибки
All Pages

Статистический ряд информации

Статистический ряд информации составляется для упрощения дальнейших расчетов в том случае, если повторность исходной информации N (количество испытанных машин) не меньше 20-25.

Для построения статистического ряда вся информация разбивается на n интервалов. Применительно к показателям надежности строительных машин n=6-12. Все интервалы должны быть одинаковыми и удобными по величине, прилегать друг к другу без разрывов.

Начало первого интервала определяется с таким расчетом, чтобы начальная точка информация находилась примерно на его середине.

Применительно к информации по доремонтным ресурсам двигателя (см. табл. 1) удобно выбрать величину интервала А=1000 мото-ч, а начало первого интервала t_см=1000 мото-ч. Далее будет дано более точное определение.

Задавшись величиной интервала А и протяженностью зоны рассеивания, число интервалов статистического ряда определяют по формуле:

,

где t_к – наработка до капитального ремонта, мото-ч.

интервалов

Статистический ряд информации составляется обычно из четырех горизонтальных строк:

в 1-й строке указывают границы каждого интервала в единицах показателя надежности;

во 2-й строке - количество случаев (частота m_i) в каждом интервале;

в 3-й строке - опытную вероятность появления показателя надежности в каждом интервале р_i;

в 4-й строке - накопленную (интегральную) опытную вероятность .

Точки, попавшие на границу интервалов, относятся к предшествующему интервалу.

В табл. 2 приведен статистический ряд информации по доремонтному ресурсу опытных двигателей.

Опытная вероятность р_i определяется как отношение числа случаев появления показателя надежности в каждом интервале m_i к повторности информации N. Так, например, опытная вероятность в третьем интервале равна:

.

Таблица 2

Статистический ряд информации по доремонтному ресурсу опытных двигатей

Интервал тыс. мото-ч.	1,0-2,0	2,0-3,0	3,0-4,0	4,0-5,0	5,0-6,0	6,0-7,0	7,0-8,0
Частота mi	2	4	25	28	10	0	1
Опытная вероятность рi;	0,03	0,06	0,36	0,40	0.14	0,00	0,01
	0,03	0,09	0,45	0,85	0,99	0,99	1,00

Среднее значение показателя надежности

Среднее значение является важнейшей характеристикой показателя надежности. На основании средних значений производится планирование работы машины, составление заявок на запасные части, определение объемов ремонтных работ и т. д.

Точность определения среднего значения возрастает по мере увеличения повторности информации, приближаясь к своему пределу - математическому ожиданию.

При обработке опытной информации в различных областях физики и математики используются различные средние значения: среднее арифметическое, среднее взвешенное, среднее гармоническое, среднее квадратическое, среднее геометрическое и т. д. При обработке опытной информации по показателям надежности тракторов, мелиоративных и строительных машин используются главным образом средние арифметические, средние взвешенные и средние гармонические значения.

Среднее арифметическое значение показателя надежности определяется по уравнению:

, (3)

где N - повторность информации (количество испытанных машин); t_i - значение i-го показателя надежности.

Уравнение (3) применяется для определения среднего значения показателя надежности в тех случаях, когда повторность исходной информации N невелика, вследствие чего ее не удается объединить в статистический ряд.

При наличии статистического ряда среднее значение показателя надежности определяется как среднее взвешенное по уравнению

, (4)

где n - количество интервалов в статическом ряду; t_ic - значение середины i-го интервала; р_i - опытная вероятность i-го интервала или его «вес».

При определении среднего значения обратных величин от основных показателей надежности t_i (износостойкость вместо скорости изнашивания детали, параметр потока отказов вместо наработки на отказ и т.д.) следует пользоваться средними гармоническими значениями , которые рассчитывают по формуле:

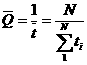. (5)

Попытки определять средние значения обратных величин по формулам (3) или (4) могут привести к значительным ошибкам.

Например, определим среднюю скорость изнашивания и среднюю износостойкость , если известны результаты испытаний трех деталей: при наработке 100 мото-ч износ составил 200 мкм; при 20 мото-ч – 160 мкм; при 30 мото-ч – 300 мкм.

Средняя скорость изнашивания детали:

мкм/мото-ч.

Средняя износостойкость детали:

мото-ч/мкм.

Средняя износостойкость детали как среднее гармоническое:

мото-ч/мкм.

Средняя износостойкость как среднее арифметическое:

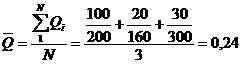мото-ч/мкм.

В последнем случае метод определения среднего значения не верен и дает по сравнению с предыдущим ( мото-ч/мкм) относительную ошибку e=60 %.

В нашем расчете при определении среднего значения доремонтного ресурса двигателя следует пользоваться формулой (4) и данными статистического ряда (табл. 2)

мото-ч.