Машиностроение и механика

Дифференциальная и интегральная функции законов распределения

Каждый закон распределения показателей надежности характеризуется двумя функциями: дифферинциальной, или функцией плотности вероятностей, и интегральной, или функцией расределения. Графическое изображение этих функций показано на рис. 8 и 9. Сравнение кривых, представленных на этих рисунках, с рис. 4 и 5 позволяет убедится в том, что дифференциальная кривая является заменителем полигона распределения, а интегральная - кривой накопленных опытных вероятностей.

По оси абсцисс дифференциальной функции откладываются значения показателя надежности, которые обычно в целях простоты табулирования нормируются по одному из параметров закона распределения. По оси ординат откладывают вероятность или количество случаев появления показателя надежности в заданном интервале его значений. Чем меньше величина интервала, тем меньше вероятность или количество показателей надежности отдельных машин будет находиться в этом интервале при прочих равных условиях. Вероятность того, что показатель надежности в результате опыта примет значение предварительно заданной постоянной величины А (см. рис. 8) равно нулю:

. (21)

Площадь под дифферинциальной кривой (т.е. сумма вероятностей всех возможных значений показателя надежности) равна единице. Площадь участка кривой t₁абt₂ составляет доли единицы вероятности и соответсвует количеству показателей надежности, попавших в интервал значений от t₁ до t₂.

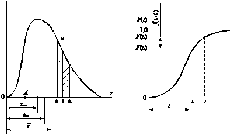
Рис. 8. Дифференциальная кривая Рис. 9. Интегральная кривая

На рис. 8 показаны среднее , модальное t_мо и медиальное t_ме значения показателя надежности. Модальной называется наиболее вероятная величина показателя надежности, медиальное - величина показателя надежности, ордината которого делит площадь под дифференциальной кривой на две равные половины.

Интегральная кривая (рис. 9) получена последовательным суммированием площадей под дифференциальной кривой в границах возможных значений показателя надежности.

По оси абсцисс интегральной кривой откладывают значения показателя надежности, а по оси ординат – суммарную вероятность или суммарное количество показателей надежности, зарегистрированных в интервале значений от нижней границы рассеивания (или от нуля) до любого произвольного значения t (см. рис. 7). Таким образом, по величине суммарной (интегральной вероятности, отложенной по оси ординат (от 0 до 1), можно определять не только количество показателей надежности (количество отказов, количество вышедших из строя машин, количество ремонтов и т. д.) в интервале от нуля до заданной величины, но и количество показателей надежности в любом, произвольно выбранном, интервале значений показателя надежности от t₁ до t₂.

Интегральная функция F(t) отражает уже реализованные показатели надежности, а интегральная функция P(t) – еще не реализованные. Применительно к показателю безотказности функция F(t) оценивает «отказность» машин (количество вышедших из строя машин или число поломок от начала эксплуатации до заданной наработки), а функция Р(t) - «безотказность» (количество машин, проработавших без поломок до заданной наработки). Функции «отказность» и «безотказность» связаны уравнением

. (22)