Машиностроение и механика

Article Index
Основы расчёта надежности мелиоративных и строительных машин
Статистический ряд информации
Абсолютные характеристики рассеивания показателей надежности
Проверка информации на выпадающие точки
Графическое изображение опытного распределения показателя надежности
коэффициент вариации
Теоретические законы распределения показателей надежности
Критерии согласия опытных и теоретических распределений показателей надежности
Укрупненный статистический ряд информации для определения критерия согласия c2
Распределение критерия Колмогорова
Дифференциальная и интегральная функции законов распределения
Закон нормального распределения показателей надежности и его практическое применение
Опытные и теоретические вероятности выхода из строя двигателей
Доверительные границы рассеивания одиночного и среднего значения показателя надежности
Пример расчета доверительных границ одиночного показателя надежности
Абсолютная и относительная предельные ошибки
All Pages

Опытные и теоретические вероятности выхода из строя двигателей

Интервал А, тыс. мото-ч	1,0 ¸ 2,0	2,0 ¸ 3,0	3,0 ¸ 4,0	4,0 ¸ 5,0	5,0 ¸ 6,0
Частота mi	2	4	25	28	10
Опытная вероятность рi	0,03	0,06	0,36	0,41	0,14
Теоретическая вероятность f(tci)	0,01	0,09	0,35	0,41	0,14
Накопленная опытная вероятность	0,03	0,09	0,45	0,86	1,00
Интегральная теоретическая вероятность F(tki)	0,01	0,11	0,46	0,85	1,00

Так как функция F₀ в данном случае отрицательна, используем уравнение (30):

.

По прил. 2 определим:

(2-я колонка, 6-я строка снизу).

Окончательно:

или 1 % двигателей потребует ремонта в интервале наработок от 0 (начало эксплуатации) до 2000 мото-ч.

Соответственно получим для конца второго интервала t_к = 3000 мото-ч:

.

По прил. 2 определим:

.

Окончательно получим:

или 11 % двигателей потребуют ремонта в интервале от начала эксплуатации до 3000 мото-ч и т.д.

Расчетные значения F(t) для всех интервалов систематического ряда для сравнения с накопленной опытной вероятностью занесем в табл. 7 (6-я колонка), а интегральную кривую F(t) наложим на кривую накопленных опытных вероятностей (см. рис. 1).

Как видно из табл. 7 и рис. 1, расхождения между опытными и теоретическими вероятностями незначительны, что подтверждает состоятельность использования в данном случае закона нормального распределения.

Анализ данных табл. 7 позволяет сделать важный практический вывод: дифференциальная вероятность в произвольно заданном интервале значений показателя надежности равна размерности интегральных вероятностей по концам этого интервала:

f(t_c)=f(t₁…t₂)=F(t₂)–F(t₁).

Эта зависимость позволяет при решении задач, связанных с определением показателя надежности, пользоваться только одной, наиболее удобной в данном случае, интегральной функцией.

Подобрав теоретический закон распределения и убедившись в его согласии с опытной информацией, представляется возможным решать ряд инженерных задач по расчету и применению показателей надежности машин и их элементов. К таким задачам относятся, например, определение количества эксплуатационных или ресурсных отказов в заданном интервале наработок, числа ремонтов машин и их агрегатов, планирование наработок или установление календарных сроков поставки отдельных машин в ремонт, определение времени и стоимости простоя машин по техническим причинам и др. Все эти задачи, как правило, решаются с использованием закона нормального распределения.

Так, например, зная параметры закона нормального распределения доремонтного ресурса двигателя, можно определить количество ресурсных отказов (количество ремонтов) у этих двигателей при их средней наработке от 4300 до 4850 мото-ч ( мото-ч, s=910 мото-ч).

Эта задача может быть решена двумя путями – по дифференциальной или интегральной функции:

1. Расчет дифференциальной функции f(t).

По уравнениям (20) и (21):

.

По прил. 2 определяем f₀(0,52) = 0,35.

Окончательно получим:

f(4300…4850)=0,60×0,35=0,21;

Таким образом 14 двигателей из 69 в этом интервале наработок будут отправлены в ремонт;

2. Расчет по интегральной функции F(t).

Для этого используем уравнения (29) и (30):

.

Определим по прил. 2:

; .

Окончательно получим:

f(2800¸3600)=0,79-0,58=0,21,

21 % двигателей потребуют ремонта в интервале наработок от 4300 до 4850 мото-ч.

Задачи подобного типа удобно решать графическим методом. Для этого в масштабе (желательно придерживаться правила «золотого сечения») строят интегральную кривую F(t) – рис. 10. В большинстве случаев интегральная кривая строится в границах , так как именно в этой зоне решаются основные задачи по определению количественных значений показателя надежности.

Интегральная кривая может быть построена по 9 точкам с координатами:

ординаты -0,5; 0,5±0,19; 0,5±0,34; 0,5±0,43; 0,5±0,48;

абсциссы -; ±0,5s; ±1,0s; ±1,5s; ±2,0s.

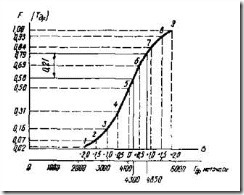
Рис. 10. Графический метод построения интегральной функции

и определения значений показателя надежности доремонтного

ресурса двигателя

Таким образом, для построения интегральной кривой можно и не пользоваться таблицей значений F(t), а записать или запомнить всего 4 цифры: 0,19; 0,34; 0,43 и 0,48.

Для того чтобы решать задачи непосредственно в размерности показателя надежности, параллельно вспомогательной оси абсцисс (размерность в долях от s) проводят основную ось абсцисс в размерности (показателя надежности (в нашем случае - мото-часы). Переход от s к размерности показателя надежности производится по величине s (в нашем случае s=910 мото-ч). При этом начальная точка вспомогательной оси абсцисс (s=0 должна быть совмещена с точкой основной абсциссы =4100 мото-ч.

На рис. 10 показан пример определения числа ремонтов двигателя (в долях единицы) при их средней наработке в интервале от 4300 до 4860 мото-ч.