Машиностроение и механика

Доверительные границы рассеивания одиночного и среднего значения показателя надежности

В результате испытания (наблюдения) совокупности машин и обработки собранной при этом информации определяются количественные характеристики показателей надежности (среднее значение , среднее квадратическое отклонение s, коэффициент вариации V и др.).

В дальнейшем значения этих характеристик должны быть перенесены на другие совокупности машин, работающих в различных условиях эксплуатации. Естественно, что изменение количества машин в совокупности и условий их эксплуатации вызовет изменение количественных характеристик показателя надежности. И хотя эти изменения носят случайный характер, они происходят в определенных границах или в определенном интервале, величина которого зависит от ряда факторов, в том числе и от количества машин в совокупности. Определение этих границ рассеивания характеристик показателей надежности, а, следовательно, и определение возможной ошибки переноса этих характеристик из одних условий в другие является одной из основных задач теории надежности.

Если было проведено наблюдение за N машинами и на этой основе определено среднее значение показателя надежности , то, как было показано выше, одиночное значение этого же показателя надежности у конкретной машины может в крайних случаях отличаться от на величину ±3s при законе нормального распределения и на величину от 0,1 а до 2,5 а при законе распределения Вейбулла (а - параметр Вейбулла).

Строго говоря, эти крайние случаи или границы рассеивания одиночного показателя надежности не охватывают все 100 % машин совокупности. Для нормального распределения площадь под дифференциальной кривой (будем в дальнейшем называть ее площадь охвата а), ограниченная протяженностью оси абсцисс ±3s, составляет 0,997 или 99,7 %. Другими словами, при таких границах рассеивания (±3s) в 997 случаях из 1000 значение одиночного показателя надежности будет находиться в интервале значений от до , и только в трех случаях из 1000 (0,3 %) значение одиночного показателя надежности может выйти за эти границы.

Нет сомнения, что такая высокая степень доверия расчета, охватывающего 99,7 % всех возможных вариантов, является излишней в подавляющем большинстве случаев при определении показателей надежности тракторов, сельскохозяйственных машин и их элементов.

Задаваясь заранее меньшими значениями площади охвата а, мы соответственно сблизим границы рассеивания одиночного показателя надежности и тем самым уменьшим возможную погрешность расчета, хотя и за счет снижения степени доверия.

Между площадью а и соответствующим этой площади интервалом рассеивания существует функциональная связь, представленная уравнением (28) и табулированная в прил. 2. Так, например, если задаться а=0,80, то при нормальном (симметричном) распределении справа от среднего значения разместится 0,40 площади. Следовательно, в прил. 2 для центрированной и нормированной функции F₀ необходимо найти ее значение, равное 0,50+0,40=0,90. Найдя это значение F₀(t)=0,90 (колонка 10, строка 14 сверху), определим количество t средних квадратических отклонений (t=1,28), которое необходимо отложить вправо и влево от среднего значения (±1,28s) для того, чтобы ограничить интервал рассеивания значений одиночного показателя надежности при заданной площади а=0,80.

Таким образом, площадь а равна в долях 1 или в % количеству одиночных показателей надежности (или количеству машин), числовые значения которых укладываются в границах соответствующего этой площади интервала.

При прочих равных условиях выбранная заранее площадь а характеризует степень доверия расчета и гарантирует вероятность попадании показателя надежности в соответствующий интервал его значений и поэтому получила название доверительная вероятность а.

Интервал, в который при заданной доверительной вероятности а попадают 100а % случаев от N, называется доверительным интервалом I_a.

И, наконец, границы, в которых может колебаться значения одиночного показателя надежности при заданной а, называются нижней доверительной границей и верхней доверительной границей .

Зависимость между принятым значением доверительной вероятности а, величинами доверительных границ и интервала I_a, возможной наибольшей ошибкой для нормального закона распределения показана на рис. 11.

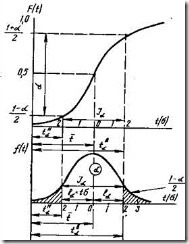
Рис. 11. Доверительная вероятность а и доверительные границы при законе нормального распределения

При определении коэффициента t (количество s) пользоваться интегральным законом нормального распределения и соответственно данными прил. 2 можно только в случае, когда повторность информации N>25, вследствие чего есть уверенность, что опытное значение s незначительно отличается от действительного. При меньших значениях повторности информации N следует пользоваться законом распределения Стьюдента и коэффициентом t_a, табулированным в прил. 2. В целях повышения точности и единообразия расчета коэффициентом Стьюдента t_а следует пользоваться и при N>25, хотя в этих случаях его отличие от t в прил. 2 весьма незначительно.

С учетом этого замечания и, пользуясь обозначениями, показанными на рис. 11, легко вывести расчетные уравнения для определения доверительного интервала I_а, доверительных границ и и абсолютной ошибки для одиночного показателя надежности:

; (31)

; (32)

; (33)

. (34)

Анализ расчетных уравнений (31) – (34) позволяет заметить, что увеличение доверительной вероятности а или, другими словами, повышение степени доверия расчета вызывает увеличение возможной ошибки расчета и расширение доверительного интервала.

Определение доверительных границ рассеивания одиночного показателя надежности дает сходные с практикой результат только в том случае, если опытные параметры выбранного закона распределения получены при достаточной повторности исходной информации.

Инженерные расчеты рассеивания одиночного показателя надежности необходимо производить при планировании сроков постановки отдельных машин или их агрегатов в ремонт, при определении остаточного ресурса отдельных деталей и сопряжений по данным микрометража и т. д., то есть во всех случаях, когда определяются характеристики показателя надежности одной машины.