Машиностроение и механика

Article Index
Основы расчёта надежности мелиоративных и строительных машин
Статистический ряд информации
Абсолютные характеристики рассеивания показателей надежности
Проверка информации на выпадающие точки
Графическое изображение опытного распределения показателя надежности
коэффициент вариации
Теоретические законы распределения показателей надежности
Критерии согласия опытных и теоретических распределений показателей надежности
Укрупненный статистический ряд информации для определения критерия согласия c2
Распределение критерия Колмогорова
Дифференциальная и интегральная функции законов распределения
Закон нормального распределения показателей надежности и его практическое применение
Опытные и теоретические вероятности выхода из строя двигателей
Доверительные границы рассеивания одиночного и среднего значения показателя надежности
Пример расчета доверительных границ одиночного показателя надежности
Абсолютная и относительная предельные ошибки
All Pages

 

Определение надежности и технологиявосстановления деталей машин

Основы расчета надежности мелиоративных и строительных машин

Из-за неудовлетворительного качества новых или отремонтированных машин при их эксплуатации, показатели надежности имеют значительные отклонения. Вследствие этого они относятся к категории случайных величин.

Вероятность появления случайной величины в конкретном опыте или в процессе испытания машин называется опытной вероятностью.

Математическую и опытную вероятности определяют по формулам:

; (1)

, (2)

где Р(А) и р(А) – соответственно математическая и опытная вероятности появления случайного события (отказа) А; М и m – соответственно расчетное и опытное число появления события А; N – общее число опытов или количество наблюдаемых машин.

Инженерную сущность опытной вероятности можно проиллюстрировать для конкретного предприятия. Возможен расчет расхода деталей на группу машин, например, бульдозеров, скреперов и т. д. Это в значительной степени приведет к экономии времени и средств на проведение ремонтов и приобретение запасных частей в ПМК, ДРСУ и т.п.

 

Обработка опытной информации по надежности мелиоративных и строительных машин

Сбор информации

Учитывая значительное рассеивание первичной информации, при испытании машин первостепенное значение имеет правильный выбор количества одновременно испытуемых машин (повторность информации).

Недостаточное количество машин при испытании может внести значительную ошибку в результаты расчетов показателей надежности и сделать их непригодными для практического использования. С другой стороны, слишком большая повторность испытаний, хотя и обеспечит высокую точность расчетов, будет неприемлема из экономических соображений вследствие высокой стоимости таких испытаний. Таким образом, необходимо подобрать оптимальное решение, при котором количество испытываемых машин, при достаточной точности конечных результатов, не будет громоздким, а сами испытания не слишком дорогими.

Информация, полученная в процессе испытания (наблюдения) машин, сводится в таблицы, которые являются основой для последующей математической обработки и расчета показателей надежности.

В качестве примера в табл. 1 приведены фактические данные по доремонтным ресурсам 70 однотипных двигателей. Эта информация в дальнейшем будет использована для обработки и расчетов показателей надежности.

Обработка информации

Принципиальные исходные положения, составляющих основу обработки информации по надежности строительных машин, следующие:

Все показатели надежности относятся к категории случайных величин.

Основными характеристиками каждого показателя надежности являются:

- среднее значение (математическое ожидание);

- характеристики рассеивания - среднее квадратическое отклонение s и коэффициент вариации V;

- доверительные границы рассеивания одиночного и среднего значений показателя надежности;

- наибольшие возможные абсолютная и относительная погрешности;

Показатели надежности являются существенными положительными величинами. В связи с этим у многих показателей свойств надежности (доремонтный, межремонтный, полный ресурсы, время восстановления, стоимость восстановления и др.) начало зоны рассеивания может существенно смещаться относительно его нулевого значения. Величину такого смещения t_см следует учитывать при определении коэффициента вариации и подборе теоретического закона распределения показателя свойств надежности.

Общая схема математической обработки опытной информации по показателям надежности и последовательность выполнения отдельных этапов представлены на рис. 1 применительно к информации по доремонтным ресурсам испытуемых двигатей (см. табл. 1);

В нижней части рис. 1 показано количество ресурсных отказов двигателей в течение каждых 1000 мото-часов их работы за весь период испытаний.

Основными этапами обработки информация являются:

составление сводной таблицы исходной информации в порядке возрастания показателя надежности (доремонтного ресурса) - (см. рис. 1);

составление статистического ряда исходной информации - (см. рис. 1);

определение среднего значения и абсолютных характеристик рассеивания (дисперсии и среднеквадратического отклонения) показателя надежности;

проверка информации на выпадающие точки;

графическое изображение опытной информации: построение гистограммы, полигона и кривой накопленных опытных вероятностей показателя надежности - 3, 4, 5 (см. рис. 1);

определение относительного показателя рассеивания показателя надежности - коэффициента вариации;

выбор теоретического закона распределения, определение его параметров и графическое построение дифференциальной и интегральной кривых - 6, 7 (см. рис. 1);

проверка совпадения опытных и теоретических законов распределения показателя надежности по критериям согласия;

определение доверительных границ рассеивания одиночных и средних значений показателя надежности и наибольших возможных ошибок расчета.

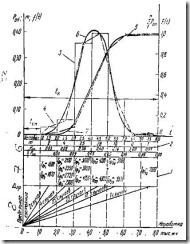
Рис. 1. Схема последовательной обработки информации

Статистический ряд информации

Статистический ряд информации составляется для упрощения дальнейших расчетов в том случае, если повторность исходной информации N (количество испытанных машин) не меньше 20-25.

Для построения статистического ряда вся информация разбивается на n интервалов. Применительно к показателям надежности строительных машин n=6-12. Все интервалы должны быть одинаковыми и удобными по величине, прилегать друг к другу без разрывов.

Начало первого интервала определяется с таким расчетом, чтобы начальная точка информация находилась примерно на его середине.

Применительно к информации по доремонтным ресурсам двигателя (см. табл. 1) удобно выбрать величину интервала А=1000 мото-ч, а начало первого интервала t_см=1000 мото-ч. Далее будет дано более точное определение.

Задавшись величиной интервала А и протяженностью зоны рассеивания, число интервалов статистического ряда определяют по формуле:

,

где t_к – наработка до капитального ремонта, мото-ч.

интервалов

Статистический ряд информации составляется обычно из четырех горизонтальных строк:

в 1-й строке указывают границы каждого интервала в единицах показателя надежности;

во 2-й строке - количество случаев (частота m_i) в каждом интервале;

в 3-й строке - опытную вероятность появления показателя надежности в каждом интервале р_i;

в 4-й строке - накопленную (интегральную) опытную вероятность .

Точки, попавшие на границу интервалов, относятся к предшествующему интервалу.

В табл. 2 приведен статистический ряд информации по доремонтному ресурсу опытных двигателей.

Опытная вероятность р_i определяется как отношение числа случаев появления показателя надежности в каждом интервале m_i к повторности информации N. Так, например, опытная вероятность в третьем интервале равна:

.

Таблица 2

Статистический ряд информации по доремонтному ресурсу опытных двигатей

Интервал тыс. мото-ч.	1,0-2,0	2,0-3,0	3,0-4,0	4,0-5,0	5,0-6,0	6,0-7,0	7,0-8,0
Частота mi	2	4	25	28	10	0	1
Опытная вероятность рi;	0,03	0,06	0,36	0,40	0.14	0,00	0,01
	0,03	0,09	0,45	0,85	0,99	0,99	1,00

Среднее значение показателя надежности

Среднее значение является важнейшей характеристикой показателя надежности. На основании средних значений производится планирование работы машины, составление заявок на запасные части, определение объемов ремонтных работ и т. д.

Точность определения среднего значения возрастает по мере увеличения повторности информации, приближаясь к своему пределу - математическому ожиданию.

При обработке опытной информации в различных областях физики и математики используются различные средние значения: среднее арифметическое, среднее взвешенное, среднее гармоническое, среднее квадратическое, среднее геометрическое и т. д. При обработке опытной информации по показателям надежности тракторов, мелиоративных и строительных машин используются главным образом средние арифметические, средние взвешенные и средние гармонические значения.

Среднее арифметическое значение показателя надежности определяется по уравнению:

, (3)

где N - повторность информации (количество испытанных машин); t_i - значение i-го показателя надежности.

Уравнение (3) применяется для определения среднего значения показателя надежности в тех случаях, когда повторность исходной информации N невелика, вследствие чего ее не удается объединить в статистический ряд.

При наличии статистического ряда среднее значение показателя надежности определяется как среднее взвешенное по уравнению

, (4)

где n - количество интервалов в статическом ряду; t_ic - значение середины i-го интервала; р_i - опытная вероятность i-го интервала или его «вес».

При определении среднего значения обратных величин от основных показателей надежности t_i (износостойкость вместо скорости изнашивания детали, параметр потока отказов вместо наработки на отказ и т.д.) следует пользоваться средними гармоническими значениями , которые рассчитывают по формуле:

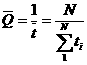. (5)

Попытки определять средние значения обратных величин по формулам (3) или (4) могут привести к значительным ошибкам.

Например, определим среднюю скорость изнашивания и среднюю износостойкость , если известны результаты испытаний трех деталей: при наработке 100 мото-ч износ составил 200 мкм; при 20 мото-ч – 160 мкм; при 30 мото-ч – 300 мкм.

Средняя скорость изнашивания детали:

мкм/мото-ч.

Средняя износостойкость детали:

мото-ч/мкм.

Средняя износостойкость детали как среднее гармоническое:

мото-ч/мкм.

Средняя износостойкость как среднее арифметическое:

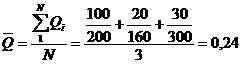мото-ч/мкм.

В последнем случае метод определения среднего значения не верен и дает по сравнению с предыдущим ( мото-ч/мкм) относительную ошибку e=60 %.

В нашем расчете при определении среднего значения доремонтного ресурса двигателя следует пользоваться формулой (4) и данными статистического ряда (табл. 2)

мото-ч.

 

Абсолютные характеристики рассеивания показателей надежности - дисперсия и среднее квадратическое отклонение

Рассеивание является важным параметром показателя надежности, позволяющей переходить от общей совокупности к показателям надежности отдельных машин. В инженерной практике эксплуатации машин на основании характеристик рассеивания показателя надежности представляется возможным решать такие важные хозяйственные задачи, как определение сроков постановки отдельных машин на ремонт и стоимости их ремонта, наименьшей и наибольшей наработки на один эксплуатационный отказ и др.

Вследствие рассеивания одиночные значения показателей надежности t_i отклоняются от своего среднего значения на величину t_i-t. Эта разность называется «отклонением», а среднее значение отклонения характеризует величину рассеивания показателя надежности

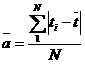, (6)

где N - повторность информации или количество испытанных машин.

Недостатком расчета рассеивания по формуле (6) является необходимость определения абсолютных значений отклонений, что при сложных расчетах может привести к ошибкам.

Более распространенной характеристикой рассеивания при испытании машин на надежность является дисперсия D, которая равна среднему значению квадратов отклонений:

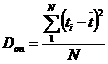, (7)

где - дисперсия, полученная в результате обработки информации по испытанию на надежность относительно небольшого количества машин.

Опытная дисперсия является смещенной по отношению к дисперсии генеральной совокупности этих же машин (т. е. очень большого их количества). Опытная и генеральная D дисперсии связаны между собой соотношением

.

Окончательно получим:

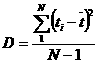. (8)

Пользоваться значением дисперсии не всегда удобно, так как абсолютная величина дисперсии получается, как правило, слишком большой и, кроме того, размерность дисперсии равна квадрату размерности показателя надежности.

В связи с этим наиболее распространенной и удобной для расчетов характеристикой рассеивания является среднее квадратическое отклонение:

. (9)

Как видно из уравнения (9), s значительно меньше по абсолютной величине, чем дисперсия, а его размерность совпадает с размерностью показателя надежности.

Дисперсия D и среднее квадратическое отклонение s являются абсолютными характеристиками рассеивания показателя надежности.

При незначительном количестве информации (N<25) среднее квадратическое отклонение определяется по уравнению:

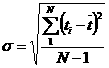. (10)

При наличии статического ряда информации (N > 25) среднее квадратическое отклонение:

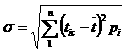. (11)

Определим по выражению (11) среднее квадратическое отклонение доремонтного ресурса двигателя:

=1000 мото-ч.

Расчеты с использованием уравнений (3) и (11) связаны с большим количеством арифметических вычислений и поэтому достаточно трудоемки.

При большом количестве информации (наличие статического ряда) для определения и s может быть рекомендован упрощенный метод расчета – метод сумм. Его сущность заключается в следующем.

Из статистического ряда выписывают две строки: значения середин интервалов и соответствующие им частоты таблица 3.

Таблица 3

Определение коэффициентов а₁, а₂, b₁ и b₂ по методу сумм

Середина интервала, мото-ч	1500	2500	3500	4500	5500	6500	7500	Примечание
Частота mi	2	4	25	28	10	0	1	N = 70
а1 = 39	2	6	31	-	11	1	1	b1 = 13
а2 = 10	2	8	-	-	-	2	1	b2 = 3

К этим строкам приписывают еще две, при этом в третьей строке, примерно на ее середине, делается прочерк одного интервала, а в четвертой строке - три прочерка: средний против прочерка третьей строки и еще два - слева и справа от него.

В третьей строке последовательно складывают частоты от начала строки до прочерка и от конца строки до прочерка. Суммы чисел подсчитывают и обозначают соответственно коэффициентами а₁ и b₁ (см. табл. 3).

В четвертой строке аналогичным образам складывают числовые значения третьей строки. Суммы чисел от начала четвертой строки до первого прочерка и от конца строки до третьего прочерка обозначают соответственно а₂ и b₂.

Среднее значение показателя надежности и среднее квадратическое отклонение определяются по уравнениям:

; (12)

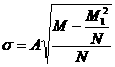, (13)

где А - величина одного интервала; t_{с -} значение середины того интервала, против которого сде­лан прочерк в третьей строке.

.

В нашем расчете:

А=1000 мото-ч;

t_с=4500 мото-ч;

;

;

мото-ч;

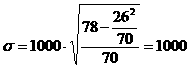мото-ч.

В литературе по теории вероятностей и теории надежности часто для определения среднего значения (математического ожидания) и среднего квадратического отклонения или дисперсии используются понятия начального и центрального моментов.

Для определения моментов статистический ряд информации представляется в виде системы расположенных на одной прямой материальных точек, массой которых является вероятность интервала р_i, а абсциссой - значение показателя надежности в середине этих интервалов t_iс.
Начальным моментом k-го порядка называется сумма произведений всех масс (р_i) на плечи (t_iс) в степени k относительно точки О.

Центральным моментом k-го порядка называется сумма произведений всех масс (р_i) на плечи в степени k относительно точки Ц (см. рис. 2).

В положении, представленном на рис. 2, система материальных точек находится в равновесии. Следовательно, начальный момент первого порядка:

.

Учитывая, что , получим:

.

Таким образом, начальный момент первого порядка равен среднему значению, или математическому ожиданию случайной величины (показателя надежности).

Определим, чему равен центральный момент второго порядка. В соответствии с формулировкой получим:

. (14)

Таким образам, центральный момент второго порядка равен дисперсии, а среднее квадратическое отклонение s — корню квадратному из центрального момента второго порядка

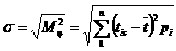. (15)

Кроме указанных основных зависимостей, центральные моменты высшего порядка характеризуют некоторые другие свойства кривых распределения. Так, например, центральный момент третьего порядка характеризует асимметрию кривой, а центральный момент четвертого порядка - эксцесс и т. д.

Проверка информации на выпадающие точки

Опытная информация по показателям надежности, полученная в процессе наблюдения за машинами в условиях рядовой эксплуатации, может иметь ошибочные точки, выпадающие из общего закона распределения. Поэтому перед окончательной математической обработкой информация должна быть проверена на выпадающие точки.

Грубая проверка информации может быть проведена визуально или по правилу ±3s. Последняя производится следующим образом: от полученного расчетным путем среднего значения показателя надежности последовательно вычитают и прибавляют 3s. Если ранние точки информации не выходят за пределы , то все точки информации считаются действительными.

Так, например, в нашем расчете, границы достоверности информации будут соответственно равны:

нижняя граница: 4150–3×1000=1150 мото-ч;

верхняя граница: 4150+3×1000=7150 мото-ч.

Наименьший доремонтный ресурс двигателя Т_др1=1600 мото-ч (см. табл. 1). Следовательно, эта точка информации действительна и должна быть учтена при дальнейших расчетах (1600>1150).

Наибольший ресурс двигателя Т_др70=7820 мото-ч. Эта точка информации выходит за верхнюю границу достоверности (7150 мото-ч). Поэтому она должна быть признана недействительной и не может быть учтена в дальнейших расчетах.

Более точная проверка как крайних, так и любых других смежных точек информации производится по критерию l (критерий Ирвина). Значения l при различном количестве информации приведены в прил. 1.

Фактическое значение критерия l_оп определяется по формуле:

, (16)

где t_i+1 и t_i - смежные точки информации.

Произведем проверку крайних точек информации по доремонтным ресурсам двигателя.

Определим l_оп для крайних точек информации:

а) для наименьшей точки информации (Т_др1=1600 мото-ч):

;

б) для наибольшей точки информации (Т_др70=7820 мото-ч):

.

Сравнение опытных и нормированных (прил. 2) критериев при N=69 позволяет заключить: первая точка информации Т_др1=1600 мото-ч является достоверной точкой (l_оп=0,27Т_др70=7820 мото-ч является выпадающей точкой (l_оп=1,85>l=1,6) и ее следует исключить из дальнейших расчетов.

В таких случаях, когда после проверки производится исключение точек информации, необходимо заново перестроить статистический ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности.

Учитывая, что последняя точка информации выпала, необходимо такой пересчет сделать и в нашем примере.

В результате пересчета для N=69 было окончательно установлено

_др=4100 мото-ч, s=910 мото-ч.

Окончательный статистический ряд информации по доремонтным ресурсам двигателя представлен в табл. 4.

Таблица 4

Статистический ряд информации по доремонтным ресурсам двигателя

Интервал, тыс. мото-ч	1,0-2,0	2,0-3,0	3,0-4,0	4,0-5,0	5,0-6,0
Частота mi	2	4	25	28	10
Опытная вероятность pi	0,03	0,06	0,36	0,41	0,14
	0,03	0,09	0,45	0,86	1,00

 

Графическое изображение опытного распределения показателя надежности

Составленный по данным исходной информации статистический ряд  дает полную характеристику опытного распределения показателя надежности.

По данным статистического ряда могут быть построены гистограмма полигон  и кривая накопленных опытных вероятностей , которые дают наглядное представление об опытном распределении показателя надежности и позволяют в первом приближении решать ряд инженерных задач, связанных с оценкой надежности строительных и мелиоративных машин.

Несколько практических рекомендаций по правилам построения графиков опытного распределения и пользования ими.

При выборе масштаба желательно придерживаться правила «золотого сечения»:

,

где Y - длина наибольшей ординаты, а Х - длина абсциссы, соответствующая наибольшему значению показателя надежности.

По оси абсцисс всех графиков откладывают в масштабе значение показателя надежности t, а по оси ординат - частоту или опытную вероятность у гистограммы и полигона и накопленная опытная вероятность у кривой накопленных вероятностей (см. рис. 3, 4 и 5).

Гистограмма является дифференциальным, а кривая накопленных опытных вероятностей - интегральным статистическими (опытными) законами распределения показателей надежности.

Площадь каждого прямоугольника гистограммы или соответствующая этому же интервалу площадь полигона определяет опытную вероятность или количество машин (в долях единицы), у которых значение показателя надежности находится в границах этого интервала.

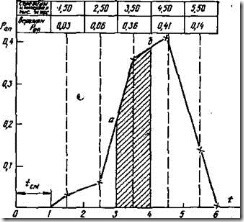
Рис. 4. Полигон распределения доремонтного ресурса двигателя

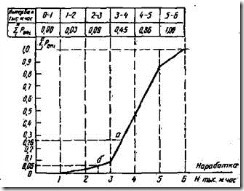
Рис. 5. Кривая накопленных опытных вероятностей

Точки полигона (см. рис. 4) образуются пересечением ординаты, равной опытной вероятности интервала, и абсциссы, равной середине этого интервала. Точки кривой накопленных опытных вероятностей (см. рис. 5) образуются пересечением ординаты, равной сумме вероятностей предыдущих интервалов, и абсциссы конца данного интервала.

Начальная и конечная точки полигона распределения приравниваются к абсциссе начала первого и конца последнего интервалов статистического ряда. Считать количественное значение ординаты за вероятность появления показателя надежности, величина которого равна абсциссе соответствующей точки, является грубой ошибкой, так как в этом случае ширина интервала равна нулю, а следовательно, и вероятность появления показателя надежности в этой точке также равна нулю.

Гистограмма и полигон, представленные на рис. 3 и 4, построены по данным испытания двигателей на доремонтный ресурс (см. табл. 1). Пользуясь этими графиками, можно определить количество двигателей, которые потребуют ремонта в заданном интервале их наработок (например от 3 до 4 тыс. мото-ч). Для этого надо определить площадь полигона или гистограммы, ограниченную заданным интервалом, которая и будет равна в процентах или долях единицы искомому количеству двигателей или числу ремонтов (площадь 3аб4 на рис. 4).

Более удобно решать задачи подобного рода с помощью интегральной кривой, показанной на рис. 5. В этом случае не требуется производить подсчет площадей - все искомые результаты определяются непосредственно по масштабу оси ординат.

Например, требуется определить количество двигателей, которые потребуют ремонта с начала эксплуатации и до их средней наработки Н=3500 мото-ч. Для этого находим ординату точки а (см. рис. 5), равную 0,26, и соответственно определим, что к наработке 3500 мото-ч 26 % (или 18 шт.) двигателей потребуют ремонта.

С помощью интегральной кривой можно рассчитывают количество двигателей, вышедших из строя в интервале наработок, например, от 2500 до 3500 мото-ч. Для этого из ординаты точки а, соответствующей Н=3500 мото-ч, надо вычесть ординату точки d, соответствующую Н=2500 мото-ч. В нашем случае 0,26-0,06=0,20 т.е. 20 % двигателей потребуют ремонта в интервале наработок от 2500 до 3600 мото-ч.

 

Относительная характеристика рассеивания показателя надежности – коэффициент вариации

Коэффициент вариации является относительной (безразмерной) характеристикой рассеивания показателя надежности, более удобной при выборе и оценке теоретического закона распределения, чем среднее квадратическое отклонение s.

Коэффициент вариации V равен отношению среднего квадратического отклонения s к среднему значению показателя надежности :

. (17)

Коэффициент вариации по уравнению (17) определяют для тех показателей надежности, зона рассеивания которых начинается от их нулевого значения или близка к нему.

При наличии смещения t_см (см. рис. 4) величину коэффициента вариации рассчитывают по формуле:

. (18)

Учет смещения особенно необходим тогда, когда величина коэффициента вариации превышает 0,33, так как в этом случае для выравнивания опытной информации используют теоретический закон распределения Вейбулла, параметры которого непосредственно зависят от величины коэффициента вариации.

Величину смещения t_см устанавливают в каждом конкретном случае. Однако при определении показателей надежности тракторов и сельскохозяйственных машин можно без ущерба для точности конечных результатов расчета пользоваться следующими практическими рекомендациями:

при наличии статистического рада за величину смещения t_см принимают значение показателя надежности в начале первого интервала (см. рис. 4);

при отсутствии статистического рада (незначительное количество исходной информации) за смещение принимать величину

.

где t₁ и t₂ - значения первого и второго показателей надежности в порядке возрастания информации.

Для доремонтного ресурса двигателя величина смещения t_см=1000 мото-ч (см. рис. 4), а величина коэффициента вариации определятся из уравнения (18):

.

Следует подчеркнуть, что смещение t_см влияет только на величину коэффициента вариации V. Величина среднего квадратического отклонения, как это видно из уравнений (10) и (11), не зависит от того, имеется или отсутствует смещение зоны рассеивания показателя надежности.

 

Теоретические законы распределения показателей надежности

Показатели свойств надежности тракторов, мелиоративных и строительных машин и их элементов определяются на основе испытания или наблюдения группы однотипных машин в условиях их нормальной эксплуатации.

Полученные значения отдельных показателей надежности должны быть в дальнейшем перенесены или на полную (генеральную) совокупность машин, в результате чего оценивается надежность данной марки машин и разрабатываются мероприятия по повышению качества их изготовления и ремонта, или на отдельные частные совокупности этих машин с целью разработки и планирования режимов их технического обслуживания и ремонта в условиях конкретного хозяйства.

Такой перенос показателей надежности от одной группы машин на другую будет правомочен только в случае достаточной массовости и достоверности первичной информации. Между тем, испытание машин связано со значительными организационными трудностями и большими материальными издержками, что неизбежно ограничивает как количество испытываемых машин, так и длительность их испытания или наблюдения. Кроме того, результаты испытания машин на надежность (количественные оценки показателей надежности) зависят от целого ряда «местных» факторов: квалификации машинистов и наблюдателей, почвенных и климатических особенностей, сортов и чистоты ГСМ, качества запасных частей и др.

Все это вместе взятое не позволяет производить прямой перенос результатов испытания на надежность других машин той же марки без соответствующих корректировок, которые заключаются в том, что для первичной информации для данной совокупности машин определяют общий теоретический закон распределения показателя надежности для генеральной совокупности машин. Этот закон выражает общий характер изменения показателя надежности машин и исключает частные отклонения, связанные с недостатками первичной информации. Такой процесс замены опытных закономерностей теоретическими называется в теории вероятностей процессом выравнивания, или сглаживания, статистической информации.

Теоретический закон распределения позволяет вести расчеты характеристик показателя надежности применительно к полной совокупности машин данной марки, а, следовательно, и к любой их частной совокупности.

В теории надежности машин и приборов используют большое количество различных законов распределения, например нормальный (Гаусса), логорифмически-нормальный, экспоненциальный, биноминальный, гамма-распределения, Пуассона, Вейбулла, Релея и некоторые другие законы.

Каждый закон имеет свою область применения, свои параметры, расчетные уравнения и таблицы, упрощающие проведение расчетов.

Применительно к показателям надежности машин, эксплуатируемых в мелиоративном строительстве, в подавляющем большинстве случаев наиболее успешно используется закон нормального распределения и закон распределения Вейбулла (экспоненциальное распределение и распределение Релея являются частными случаями закона Вейбулла).

Окончательный выбор закона распределения зависит от величины коэффициента вариации: если V>0,5, выбирают закон распределения Вейбулла, если V<0,33 – закон нормального распределения. В случае когда 0,5³V>0,3, то выбор закона распределения осуществляется на основании критерия согласия.

 

Критерии согласия опытных и теоретических распределений показателей надежности

Выбор теоретического закона распределения показателя надежности производится, как это было показано выше, в соответствии с областью применения и с учетом величины коэффициента вариации.

Совмещение в одном масштабе опытной и теоретической дифференциальных кривых (полигон распределения и кривая плотности вероятности) позволяет визуально судить о степени их совпадения или согласия.

Однако в некоторых случаях нужны более точные и объективные методы оценки совпадения опытных и теоретических данных по так называемым «критериям согласия». В частности, такая проверка необходима в тех случаях, когда величина коэффициента вариации близка к 0,33, вследствие чего рассеивание показателя надежности может быть подчинено как закону нормального распределения, так и закону распределения Вейбулла. В таких случаях предпочтение тому или иному закону распределения показателя надежности может быть сделано только на основе критерия согласия.

Физический смысл проверки «согласия» заключается в том, чтобы определить степень расхождения опытной и теоретической вероятностей. При этом в качестве меры совпадения или расхождения могут быть выбраны различные критерии согласия: сумма квадратов отклонения теоретических вероятностей от опытных, наибольшее или суммарное отклонение кривой накопленных опытных вероятностей от интегральной кривой теоретического закона распределения и т. д.

Критерий согласия является случайной величиной и, следовательно, подчиняется определенному закону распределения. Поэтому по величине критерия согласия в каждом конкретном случае можно определить вероятность совпадения опытных и теоретических функций и на этом основании принять или отбросить выбранный теоретический закон распределения показателя надежности. Однако при этом следует иметь в виду, что как бы не велика была вероятность совпадения, она свидетельствует только о том, что выбранный закон не противоречит опытным данным, но не может явиться гарантией того, что этот закон в данном случае лучше, чем какой-либо другой выравнивает опытную информацию.

Поэтому наиболее удачно используются критерии согласия в тех случаях, как это было в примере с доремонтными ресурсами двигателя, когда необходимо выбрать один теоретический закон распределения из двух или нескольких. В этом случае можно не сомневаться, что наиболее приемлемым окажется тот закон распределения, совпадение которого с опытной информацией характеризуется наименьшей величиной расхождения.

В теории вероятностей известно несколько критериев согласия. Применительно к показателям надежности строительных и мелиоративных машин чаще используются критерий Пирсона c² или критерий Колмогорова.

Критерий c² определяется как сумма квадратов отклонений опытных и теоретических частот в каждом интервале статистического ряда информации:

, (19)

где n - число интервалов в статистическом ряду; m_опi - опытная частота (количество случаев) в i-ом интервале статистического ряда; m_Тi - теоретическая частота в i-ом интервале;

, (20)

где N - общее количество испытываемых машин или повторность информации.

Для определения критерия согласия c² строится укрупненный статистический ряд информации при условии:

m_i³5 и n³4.

При построении укрупненного статистического ряда допускается объединение тех интервалов, в которых число случаев m_i<5. В целях уменьшения количества арифметических вычислений не рекомендуется увеличивать число интервалов n больше 7. Так, при расчете доремонтных ресурсов двигателя удобный для определения критерия согласия c² укрупненный статистический ряд приведен ниже в табл. 5.

В 3- и 4-ой строках укрупненного статистического ряда приведены значения теоретических частот соответственно закону нормального распределения и закону распределения Вейбулла, подсчитанных по прил. 2.

Таблица 5

 

Укрупненный статистический ряд информации для определения критерия согласия c²

Интервал, тыс. мото-ч	До 3,0	3,0-4,0	4,0-5,0	Свыше 5,0
Опытная частота mопi	6	25	28	10
Закон нормального распределения mТi	8.3	23,4	26.3	11.0
Закон Вейбулла mТi	9,6	22,8	24,8	11,8

Даже визуально можно заметить, что закон нормального распределения в данном случае обеспечивает лучшее совпадение с опытной информацией.

Критерий c² будет соответственно равен:

для закона нормального распределения

для закона распределения Вейбулла

Судя по значениям критериев согласия, приходим к окончательному выводу о том, что применительно к доремонтным ресурсам двигателя более приемлемым является закон нормального распределения.

Пользуясь критерием согласия c², можно по приложению 2 определить вероятность совпадения опытных и теоретических данных. Естественно, что вероятность совпадения при прочих равных условиях зависит также и от повторности использованной информации. Поэтому для входа в таблицу приложения необходимо определить число «степеней свободы» по уравнению:

где n - число интервалов укрупненного статистического ряда; k - число обязательных «связей».

Для распределения по закону Вейбулла, так же как и для закона нормального распределения, число обязательных связей равно трем: две связи - два параметра распределения и третья связь:

.

 

Таким образом, в нашем растете:

.

Следовательно, значения критерия c² ищем в 1-й строке, а вероятности совпадения определяем в заглавной строке (значение р) прил. 2.

Находим, что вероятность совпадения закона нормального распределения (c²=0,95) составляет более 0,3 или более 30 %, а закона Вейбулла (c²=2,26) менее 0,15 или менее 15 %.

Следует помнить, что критической вероятностью совпадения принято считать p=0,1. В случае если р<0,1, выбранный для выравнивания теоретический закон распределения следует считать недействительным.

Оценку совпадения проще производить по критерию Колмогорова. В этом случае в качестве меры совпадения выбрана наибольшая разность Б между статистической и теоретической интегральными функциями распределения:

,

где и - соответственно сумма накопленных опытных вероятностей и интегральная функция теоретического закона распределения при таком значении показателя надежности t, при котором Б=max.

Для учета повторности информации Колмогоров определяет критерий согласия l по уравнению:

,

где N - общее количество информации.

Распределение критерия Колмогорова

l	0,0	0,5	0,7	0,8	0,9	1,0	1,1	1,2	1,3
Р(l)	1,0	0,96	0,71	0,54	0,39	0,27	0,18	0,11	0,07

В нашем примере получим для закона нормального распределения.

;

.

По табл. 6 находим: Р(l)»0,96 или опытные и теоретические данные совпадают на 96 %.

Критерий Колмогорова следует применять только в тех случаях, когда известен заранее не только теоретический закон распределения, но и значения его параметров. При определении показателей надежности мелиоративных и строительных машин такой случай практически невозможен (параметры распределения определяются по опытной информации), рис. 7.

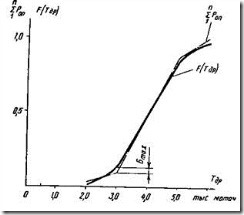
Рис. 7. Оценка совпадения по критерию Колмогорова

Поэтому для оценки совпадения опытных и теоретических значений показателей надежности следует использовать критерий c², так как критерий Колмогорова дает, как правило, значительно завышенную вероятность совпадения, как например, в случае определения доремонтного ресурса двигателя.

Следует подчеркнуть это обстоятельство, так как многие инженеры-испытатели строительных машин часто пользуются критерием Колмогорова из-за простоты его определения.

 

Дифференциальная и интегральная функции законов распределения

Каждый закон распределения показателей надежности характеризуется двумя функциями: дифферинциальной, или функцией плотности вероятностей, и интегральной, или функцией расределения. Графическое изображение этих функций показано на рис. 8 и 9. Сравнение кривых, представленных на этих рисунках, с рис. 4 и 5 позволяет убедится в том, что дифференциальная кривая является заменителем полигона распределения, а интегральная - кривой накопленных опытных вероятностей.

По оси абсцисс дифференциальной функции откладываются значения показателя надежности, которые обычно в целях простоты табулирования нормируются по одному из параметров закона распределения. По оси ординат откладывают вероятность или количество случаев появления показателя надежности в заданном интервале его значений. Чем меньше величина интервала, тем меньше вероятность или количество показателей надежности отдельных машин будет находиться в этом интервале при прочих равных условиях. Вероятность того, что показатель надежности в результате опыта примет значение предварительно заданной постоянной величины А (см. рис. 8) равно нулю:

. (21)

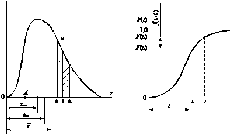Площадь под дифферинциальной кривой (т.е. сумма вероятностей всех возможных значений показателя надежности) равна единице. Площадь участка кривой t₁абt₂ составляет доли единицы вероятности и соответсвует количеству показателей надежности, попавших в интервал значений от t₁ до t₂.

Рис. 8. Дифференциальная кривая Рис. 9. Интегральная кривая

На рис. 8 показаны среднее , модальное t_мо и медиальное t_ме значения показателя надежности. Модальной называется наиболее вероятная величина показателя надежности, медиальное - величина показателя надежности, ордината которого делит площадь под дифференциальной кривой на две равные половины.

Интегральная кривая (рис. 9) получена последовательным суммированием площадей под дифференциальной кривой в границах возможных значений показателя надежности.

По оси абсцисс интегральной кривой откладывают значения показателя надежности, а по оси ординат – суммарную вероятность или суммарное количество показателей надежности, зарегистрированных в интервале значений от нижней границы рассеивания (или от нуля) до любого произвольного значения t (см. рис. 7). Таким образом, по величине суммарной (интегральной вероятности, отложенной по оси ординат (от 0 до 1), можно определять не только количество показателей надежности (количество отказов, количество вышедших из строя машин, количество ремонтов и т. д.) в интервале от нуля до заданной величины, но и количество показателей надежности в любом, произвольно выбранном, интервале значений показателя надежности от t₁ до t₂.

Интегральная функция F(t) отражает уже реализованные показатели надежности, а интегральная функция P(t) – еще не реализованные. Применительно к показателю безотказности функция F(t) оценивает «отказность» машин (количество вышедших из строя машин или число поломок от начала эксплуатации до заданной наработки), а функция Р(t) - «безотказность» (количество машин, проработавших без поломок до заданной наработки). Функции «отказность» и «безотказность» связаны уравнением

. (22)

Закон нормального распределения показателей надежности и его практическое применение

Закон нормального распределения (закон Гаусса) широко используется во многих отраслях науки и техники. Применительно к показателям надежности тракторов, сельскохозяйственных машин и их элементов закон нормального распределения (ЗНР) используется в случаях:

определения характеристик рассеивания полных, доремонтных и межремонтных ресурсов машин, их агрегатов и узлов;

определения характеристик рассеивания (времени и стоимости восстановления работоспособности машины и ее элементов;

определения характеристик рассеивания наработок на один ресурсный отказ;

определения характеристик рассеивания ошибок измерения и размеров деталей в пределах допуска;

сложения нескольких одинаковых или разных законов распределения.

Приведенные случаи применения ЗНР не являются обязательными. Иногда рассеивание перечисленных показателей надежности подчинено другим законам распределения. Поэтому в каждом конкретном случае расчета необходимо производить проверку правильности выбора закона распределения.

Закон нормального распределения, как и все другие законы, характеризуется дифференциальной ¦(t) и интегральной F(t) функциями. Отличительной особенностью этих функций является симметричное рассеивание частных значений показателей надежности относительно среднего значения.

Дифференциальная функция (или плотность вероятности нормального распределения) определяется по уравнению:

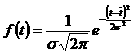, (23)

где е - основание натурального логарифма (е=2,718); p - 3,14; - среднее значение показателя надежности; s - среднее квадратическое отклонение.

Если в уравнении (23) среднее значение показателя надежности приравнять нулю, а среднее квадратическое отклонение s - единице, то получим выражение для центрированной дифференциальной функции:

. (24)

Центрированная функция (19) табулирована при условии нормирования показателя надежности в долях среднего квадратического отклонения s. В прил. 2 даны значения центрированной и нормированной дифференциальной функции нормального распределения ¦₀(t).

Из уравнений (18) и (19) получим:

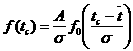. (25)

Следовательно:

, (26)

где t_с - среднее значение показателя надежности в заданном интервале А или значение середины интервала статистического ряда; А - величина заданного интервала значений показателя надежности или величина интервала статистического ряда.

При проведении инженерных расчетов характеристик надежности следует пользоваться уравнением (25) и табл. 1 прил. с учетом зависимости (26).

Интегральную функцию или функция распределения F(t) получают интегрированием функции плотности вероятности ¦(t)

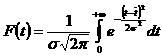. (27)

Центрированная и нормированная интегральная функция (s=1,0 и =0) определяется уравнением:

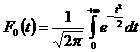. (28)

Центрированная интегральная функция F₀(t) табулирована, ее значения приведены в прил. 2.

Из уравнений (27) и (28) получим:

. (29)

где t_{к -} значение заданного показателя надежности или конца интервала статистического рада.

Из уравнения (28) следует, что

. (30)

При расчете характеристик показателей надежности следует пользоваться уравнениями (29) и (30), определяя при этом значение F₀(t) по прил. 2.

Покажем применение закона нормального распределения в целях выравнивания опытной информации на примере результатов испытания двигателей на доремонтный ресурс (см. табл. 1).

В результате первичной обработки информации было установлено:

средний доремонтный ресурс Т_др=4100 мото-ч;

среднее квадратическое отклонение s=910 мото-ч;

коэффициент вариации V=0,32.

С учетом величины коэффициента вариации (0,32<0,33) заменяем опытное статистическое распределение функциями закона нормального распределения с параметрами Т_др=4100 мото-ч и s=910 мото-ч.

Для того чтобы убедиться в совпадении статистического и выбранного теоретического законов распределения доремонтного ресурса двигателя, построим теоретические дифференциальную и интегральную кривые и наложим их соответственно на полигон и кривую накопленных опытных вероятностей (см. рис. 1).

Для построения дифференциальной кривой ¦(t) определим теоретическую вероятность или количество двигателей (в долях единицы), которые потребуют ремонта в каждом интервале статистического ряда (см. табл. 4).

Рассчитаем количество двигателей, вышедших из строя в интервале их наработок от 1000 до 2000 мото-ч (середина интервала t_с=1500 мото-ч).

Согласно (25) и (26):

.

Определим значение ¦₀(2,86) по прил. 2 и 8-я колонка, 2-я строка снизу): ¦₀(2,86)=0,007.

Окончательно получим:

¦(1000…2000)=1,10×0,007=0,01,

т.е. 1 % двигателей необходимо ремонтировать в интервале наработок от 1000 до 2000 мото-ч.

Соответственно для интервала от 2000 до 3000 мото-ч (t_с=2500 мото-ч):

,

или 9 % двигателей потребуют ремонта в этом интервале наработок.

Для интервала от 3000 до 4000 мото-ч получим:

и т. д.

Расчетные теоретические вероятности для сравнения с опытной вероятностью заносим в табл. 7 по каждому интервалу статистического ряда (4-я строка), а дифференциальную кривую ¦(t) наложим на полигон (рис. 1).

Для построения интегральной кривой F(t) определим значения ординат по концам интервалов статистического ряда. Так, например, для конца 1-го интервала (t_к = 2000 мото-ч) согласно (24):

.

Опытные и теоретические вероятности выхода из строя двигателей

Интервал А, тыс. мото-ч	1,0 ¸ 2,0	2,0 ¸ 3,0	3,0 ¸ 4,0	4,0 ¸ 5,0	5,0 ¸ 6,0
Частота mi	2	4	25	28	10
Опытная вероятность рi	0,03	0,06	0,36	0,41	0,14
Теоретическая вероятность f(tci)	0,01	0,09	0,35	0,41	0,14
Накопленная опытная вероятность	0,03	0,09	0,45	0,86	1,00
Интегральная теоретическая вероятность F(tki)	0,01	0,11	0,46	0,85	1,00

Так как функция F₀ в данном случае отрицательна, используем уравнение (30):

.

По прил. 2 определим:

(2-я колонка, 6-я строка снизу).

Окончательно:

или 1 % двигателей потребует ремонта в интервале наработок от 0 (начало эксплуатации) до 2000 мото-ч.

Соответственно получим для конца второго интервала t_к = 3000 мото-ч:

.

По прил. 2 определим:

.

Окончательно получим:

или 11 % двигателей потребуют ремонта в интервале от начала эксплуатации до 3000 мото-ч и т.д.

Расчетные значения F(t) для всех интервалов систематического ряда для сравнения с накопленной опытной вероятностью занесем в табл. 7 (6-я колонка), а интегральную кривую F(t) наложим на кривую накопленных опытных вероятностей (см. рис. 1).

Как видно из табл. 7 и рис. 1, расхождения между опытными и теоретическими вероятностями незначительны, что подтверждает состоятельность использования в данном случае закона нормального распределения.

Анализ данных табл. 7 позволяет сделать важный практический вывод: дифференциальная вероятность в произвольно заданном интервале значений показателя надежности равна размерности интегральных вероятностей по концам этого интервала:

f(t_c)=f(t₁…t₂)=F(t₂)–F(t₁).

Эта зависимость позволяет при решении задач, связанных с определением показателя надежности, пользоваться только одной, наиболее удобной в данном случае, интегральной функцией.

Подобрав теоретический закон распределения и убедившись в его согласии с опытной информацией, представляется возможным решать ряд инженерных задач по расчету и применению показателей надежности машин и их элементов. К таким задачам относятся, например, определение количества эксплуатационных или ресурсных отказов в заданном интервале наработок, числа ремонтов машин и их агрегатов, планирование наработок или установление календарных сроков поставки отдельных машин в ремонт, определение времени и стоимости простоя машин по техническим причинам и др. Все эти задачи, как правило, решаются с использованием закона нормального распределения.

Так, например, зная параметры закона нормального распределения доремонтного ресурса двигателя, можно определить количество ресурсных отказов (количество ремонтов) у этих двигателей при их средней наработке от 4300 до 4850 мото-ч ( мото-ч, s=910 мото-ч).

Эта задача может быть решена двумя путями – по дифференциальной или интегральной функции:

1. Расчет дифференциальной функции f(t).

По уравнениям (20) и (21):

.

По прил. 2 определяем f₀(0,52) = 0,35.

Окончательно получим:

f(4300…4850)=0,60×0,35=0,21;

Таким образом 14 двигателей из 69 в этом интервале наработок будут отправлены в ремонт;

2. Расчет по интегральной функции F(t).

Для этого используем уравнения (29) и (30):

.

Определим по прил. 2:

; .

Окончательно получим:

f(2800¸3600)=0,79-0,58=0,21,

21 % двигателей потребуют ремонта в интервале наработок от 4300 до 4850 мото-ч.

Задачи подобного типа удобно решать графическим методом. Для этого в масштабе (желательно придерживаться правила «золотого сечения») строят интегральную кривую F(t) – рис. 10. В большинстве случаев интегральная кривая строится в границах , так как именно в этой зоне решаются основные задачи по определению количественных значений показателя надежности.

Интегральная кривая может быть построена по 9 точкам с координатами:

ординаты -0,5; 0,5±0,19; 0,5±0,34; 0,5±0,43; 0,5±0,48;

абсциссы -; ±0,5s; ±1,0s; ±1,5s; ±2,0s.

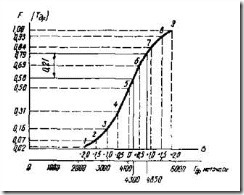
Рис. 10. Графический метод построения интегральной функции

и определения значений показателя надежности доремонтного

ресурса двигателя

Таким образом, для построения интегральной кривой можно и не пользоваться таблицей значений F(t), а записать или запомнить всего 4 цифры: 0,19; 0,34; 0,43 и 0,48.

Для того чтобы решать задачи непосредственно в размерности показателя надежности, параллельно вспомогательной оси абсцисс (размерность в долях от s) проводят основную ось абсцисс в размерности (показателя надежности (в нашем случае - мото-часы). Переход от s к размерности показателя надежности производится по величине s (в нашем случае s=910 мото-ч). При этом начальная точка вспомогательной оси абсцисс (s=0 должна быть совмещена с точкой основной абсциссы =4100 мото-ч.

На рис. 10 показан пример определения числа ремонтов двигателя (в долях единицы) при их средней наработке в интервале от 4300 до 4860 мото-ч.

Доверительные границы рассеивания одиночного и среднего значения показателя надежности

В результате испытания (наблюдения) совокупности машин и обработки собранной при этом информации определяются количественные характеристики показателей надежности (среднее значение , среднее квадратическое отклонение s, коэффициент вариации V и др.).

В дальнейшем значения этих характеристик должны быть перенесены на другие совокупности машин, работающих в различных условиях эксплуатации. Естественно, что изменение количества машин в совокупности и условий их эксплуатации вызовет изменение количественных характеристик показателя надежности. И хотя эти изменения носят случайный характер, они происходят в определенных границах или в определенном интервале, величина которого зависит от ряда факторов, в том числе и от количества машин в совокупности. Определение этих границ рассеивания характеристик показателей надежности, а, следовательно, и определение возможной ошибки переноса этих характеристик из одних условий в другие является одной из основных задач теории надежности.

Если было проведено наблюдение за N машинами и на этой основе определено среднее значение показателя надежности , то, как было показано выше, одиночное значение этого же показателя надежности у конкретной машины может в крайних случаях отличаться от на величину ±3s при законе нормального распределения и на величину от 0,1 а до 2,5 а при законе распределения Вейбулла (а - параметр Вейбулла).

Строго говоря, эти крайние случаи или границы рассеивания одиночного показателя надежности не охватывают все 100 % машин совокупности. Для нормального распределения площадь под дифференциальной кривой (будем в дальнейшем называть ее площадь охвата а), ограниченная протяженностью оси абсцисс ±3s, составляет 0,997 или 99,7 %. Другими словами, при таких границах рассеивания (±3s) в 997 случаях из 1000 значение одиночного показателя надежности будет находиться в интервале значений от до , и только в трех случаях из 1000 (0,3 %) значение одиночного показателя надежности может выйти за эти границы.

Нет сомнения, что такая высокая степень доверия расчета, охватывающего 99,7 % всех возможных вариантов, является излишней в подавляющем большинстве случаев при определении показателей надежности тракторов, сельскохозяйственных машин и их элементов.

Задаваясь заранее меньшими значениями площади охвата а, мы соответственно сблизим границы рассеивания одиночного показателя надежности и тем самым уменьшим возможную погрешность расчета, хотя и за счет снижения степени доверия.

Между площадью а и соответствующим этой площади интервалом рассеивания существует функциональная связь, представленная уравнением (28) и табулированная в прил. 2. Так, например, если задаться а=0,80, то при нормальном (симметричном) распределении справа от среднего значения разместится 0,40 площади. Следовательно, в прил. 2 для центрированной и нормированной функции F₀ необходимо найти ее значение, равное 0,50+0,40=0,90. Найдя это значение F₀(t)=0,90 (колонка 10, строка 14 сверху), определим количество t средних квадратических отклонений (t=1,28), которое необходимо отложить вправо и влево от среднего значения (±1,28s) для того, чтобы ограничить интервал рассеивания значений одиночного показателя надежности при заданной площади а=0,80.

Таким образом, площадь а равна в долях 1 или в % количеству одиночных показателей надежности (или количеству машин), числовые значения которых укладываются в границах соответствующего этой площади интервала.

При прочих равных условиях выбранная заранее площадь а характеризует степень доверия расчета и гарантирует вероятность попадании показателя надежности в соответствующий интервал его значений и поэтому получила название доверительная вероятность а.

Интервал, в который при заданной доверительной вероятности а попадают 100а % случаев от N, называется доверительным интервалом I_a.

И, наконец, границы, в которых может колебаться значения одиночного показателя надежности при заданной а, называются нижней доверительной границей и верхней доверительной границей .

Зависимость между принятым значением доверительной вероятности а, величинами доверительных границ и интервала I_a, возможной наибольшей ошибкой для нормального закона распределения показана на рис. 11.

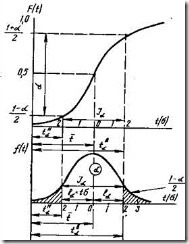
Рис. 11. Доверительная вероятность а и доверительные границы при законе нормального распределения

При определении коэффициента t (количество s) пользоваться интегральным законом нормального распределения и соответственно данными прил. 2 можно только в случае, когда повторность информации N>25, вследствие чего есть уверенность, что опытное значение s незначительно отличается от действительного. При меньших значениях повторности информации N следует пользоваться законом распределения Стьюдента и коэффициентом t_a, табулированным в прил. 2. В целях повышения точности и единообразия расчета коэффициентом Стьюдента t_а следует пользоваться и при N>25, хотя в этих случаях его отличие от t в прил. 2 весьма незначительно.

С учетом этого замечания и, пользуясь обозначениями, показанными на рис. 11, легко вывести расчетные уравнения для определения доверительного интервала I_а, доверительных границ и и абсолютной ошибки для одиночного показателя надежности:

; (31)

; (32)

; (33)

. (34)

Анализ расчетных уравнений (31) – (34) позволяет заметить, что увеличение доверительной вероятности а или, другими словами, повышение степени доверия расчета вызывает увеличение возможной ошибки расчета и расширение доверительного интервала.

Определение доверительных границ рассеивания одиночного показателя надежности дает сходные с практикой результат только в том случае, если опытные параметры выбранного закона распределения получены при достаточной повторности исходной информации.

Инженерные расчеты рассеивания одиночного показателя надежности необходимо производить при планировании сроков постановки отдельных машин или их агрегатов в ремонт, при определении остаточного ресурса отдельных деталей и сопряжений по данным микрометража и т. д., то есть во всех случаях, когда определяются характеристики показателя надежности одной машины.

Пример расчета доверительных границ одиночного показателя надежности

Расчет 1.2. В ПМК имеется 12 бульдозеров ДЗ-42, на которых установлены новые двигатели СМД-17. Требуется определять, в каком диапазоне наработок будет производиться ремонт этих двигателей (доверительные границы рассеивания доремонтного ресурса), если известно, что рассеивание доремонтных ресурсов двигателей подчинено закону нормального распределения с параметрами:

мото-ч, s=910 мото-ч.

Доверительной вероятностью задаемся а=0,90.

Порядок расчета.

1) Определим по прил. 2 значение коэффициента t_а для а=0,90 и N=12

t_a=1,80.

2) Определим по уравнениям (32) и (33) доверительные границы наработок до постановки двигателей в ремонт:

мото-ч.

мото-ч.

Доверительный интервал I_а, определим по уравнению (34)

мото-ч.

В случае распределения Вейбулла определение доверительных границ рассеивания одиночного показателя надежности производится по такой же принципиальной схеме, как и при законе нор­мального распределения.

Наиболее характерным и имеющим большое практическое значение примером использования закона распределения Вейбулла является определение доверительных границ остаточного ресурса Т₀ конкретной детали или сопряжения, если известны параметры распределения или хотя бы опытный коэффициент вариации V.

Все сказанное выше относится только к определению доверительных границ одиночного показателя надежности.

В практике чаще приходится встречаться с расчетом доверительных границ среднего значения показателя надежности.

Расчетная схема и физический смысл доверительных границ при заданной доверительной вероятности а для среднего значения показателя надежности остаются такими же, как и для одиночного показателя (см. рис. 11 и 12).

Разница заключена в определении величины среднего квадратического отклонения.

Если представить, что было проведено n испытаний совокупностей из N машин и в каждом случае определялись средние значения показателя надежности , то ясно, что эти средние будут отличаться друг от друга по величине, рассеиваясь вокруг истинного, но неизвестного нам, математического ожидания. Рассеивание средних значений , естественно, будет тем больше, чем меньше число машин N участвовало при каждом испытании. Однако даже при самых малых значениях N среднее квадратическое отклонение этих средних значений будет меньше среднего квадратического отклонения одиночного показателя надежности s. Связь между и s установлена в теории вероятностей:

. (35)

Таким образом, по аналогии с (31)-(34) и с учетом (30) расчётными уравнениями для определения рассеивания среднего значения показателя надежности при законе нормального распределения и заданной доверительной вероятности а являются:

абсолютная ошибка:

; (36)

нижняя доверительная граница:

; (37)

верхняя доверительная граница

; (38)

доверительный интервал

. (39)

Рис. 12. Доверительные границы остаточного ресурса детали или сопряжения при распределении Вейбулла

Расчет 2.2. На основании проведенных испытаний 69 новых двигателей СМД-17 было установлено, что рассеивание их доремонтного ресурса подчинено закону нормального распределения с параметрами мото-ч и s=910 мото-ч.

Спрашивается:

а) если вновь провести испытания таких же 69 двигателей, то в каких пределах может измениться их средний доремонтный ресурс?

б) в хозяйстве одновременно работают 12 новых двигателей СМД-17. При планировании их загрузки в каких пределах сле­дует учитывать возможные изменения величины среднего доремонтного ресурса, если известны результаты испытания 69 двигателей?

Для решения этих задач зададимся доверительной вероятностью а=0,90 и определим коэффициент Стьюдента t_a (прил. 2):

для случая «a» t_a=1,67,

для случая «б» t_a=1,80.

По уравнениям (37) и (38) определим доверительные границы рассеивания доремонтного ресурса двигателя СМД-17:

для случая «а»

мото-ч,

мото-ч;

для случая «б»

мото-ч,

мото-ч,

Как и следовало ожидать, доверительные границы у доремонтного ресурса двигателя СМД-17 во втором случае (случай «б») вследствие меньшего количества машин в хозяйстве (N=12) будут шире, чем при N=69.

Аналогично определяют доверительные границы рассеивания среднего значения показателя надежности при законе Вейбулла.

Приведем без выводов уравнения для определения доверительных границ по Вейбуллу при заданной доверительной вероятности а с учетом и без учета смещения начала рассеивания t_см.

а) С учетом смещения нижняя и верхняя доверительные границы рассеивания показателя надежности определяются по уравнениям:

; (40)

. (41)

б) Без учета смещения доверительные границы определяются по уравнениям:

; (42)

, (43)

где r₁ и r₃ - коэффициенты Вейбулла, определяемые по прил. 2 в зависимости от заданной величины доверительной вероятности а и повторности информации N.

Применительно к основному расчету ( мото-ч, b=3,0, t_см=1500 мото-ч), задавшись доверительной вероятностью а= 0,90, по табл. прил. 3 (для N=69) определим:

r₁=1,18; r₃=0,86.

Доверительные границы среднего доремонтного ресурса будут соответственно равны уравнения (40) и (41):

мото-ч;

мото-ч.

В отличие от закона нормального распределения доверительные границы при распределении Вейбулла асимметричны среднему значению показателя надежности : верхняя граница отличается от среднего значения на большую величину, чем нижняя.

В практике часто приходится определять односторонние доверительные границы: верхнюю или нижнюю. Так, например, в технических условиях на новую или отремонтированную машину (агрегат) указывают, что средний доремонтный (межремонтный) ресурс должен превышать заданный гарантийный ресурс при до верительной вероятности а.

Будем считать, что заданный гарантийный ресурс является нижней доверительной границей среднего ресурса (в этом случае верхняя граница не указывается).

Для решения этой задачи следует считать, что вся площадь за нижней границей равна а, а до нижней границы - соответственно 1-а (при двусторонних доверительных границах слева от нижней и справа от верхней границ располагались площади, равные ).

Таким же образом распределяются площади и при односторонней верхней доверительной границе (правее верхней границы площадь равна 1-а).

На этом основании при определении односторонних доверительных границ следует пользоваться теми же уравнениями, что и при определении двусторонних доверительных границ, только значения коэффициентов t_а, r₃, и r₁ следует брать в прил. 2 на колонку левее. Например, при заданной дове­рительной вероятности а=0,90 значения t_a, r₁ и r₃ надо брать из колонки для а=0,80; при заданной доверительной вероятности а=0,95 значения t_а, r₁ и r₃ следует брать из колонки для а=0,90 и т. д.

Для того чтобы не путать обозначения в дальнейшем при определении односторонних доверительных границ, коэффициенты будут обозначаться: t_0a, r₀₁ и r₀₃.

Расчет 3.2. Определить нижнюю одностороннюю доверительную границу доремонтного ресурса двигателя при законе нормального распределения ( мото-ч, s=910 мото-ч) при доверительной вероятности а=0,90.

По прил. 2 для N=69 определим, что t_0a =1,29 (а не 1,67, как при двусторонних доверительных границах).

По уравнению (37) рассчитаем нижнюю одностороннюю доверительную границу:

мото-ч.

Верхняя односторонняя доверительная граница при а=0,90 будет равна (уравнение 38)

мото-ч.

При переносе результатов испытания машин из одной совокупности в другую или в другие условия эксплуатации может изменяться не только среднее значение показателя надежности, но и опытное значение его среднего квадратического отклонения s.

Двусторонние доверительные границы рассеивания s при заданной доверительной вероятности а для закона нормального распределения определяются по уравнениям:

; (44)

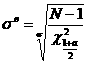; (45)

где c² - коэффициент Пирсона (определяется по прил. 2).

При законе распределения Вейбулла могут быть определены доверительные границы параметров а и b (ГОСТ 17509-72).

Абсолютная и относительная предельные ошибки

Числовые значения характеристик показателя надежности меняются в зависимости от количества наблюдаемых машин N и условий их эксплуатации. Оцениваются эти изменения доверительными границами или доверительным интервалом.

Однако часто при расчетах характеристик показателя надежности и переносе их на другие совокупности машин возникает необходимость оценить возможную наибольшую (предельную) ошибку такого переноса.

Как видно из рис. 11 и 12, доверительный интервал перекрывает истинное среднее значение (математическое ожидание) показателя надежности с доверительной вероятностью а. Поэтому наибольшая возможная ошибка переноса опытных характеристик показателя надежности при заданной доверительной вероятности а будет:

.

Для большей наглядности удобнее оперировать относительной предельной ошибкой e_а в процентах от среднего значения показателя надежности , которая независимо от выбранного закона распределения определится из уравнения:

. (46)

Так, например, при определении среднего доремонтного ресурса двигателя СМД-17 по закону Вейбулла для N=69 и a=0,90 относительная ошибка может достигать предельной величины:

.