Машиностроение и механика

Article Index
Основы расчёта надежности мелиоративных и строительных машин
Статистический ряд информации
Абсолютные характеристики рассеивания показателей надежности
Проверка информации на выпадающие точки
Графическое изображение опытного распределения показателя надежности
коэффициент вариации
Теоретические законы распределения показателей надежности
Критерии согласия опытных и теоретических распределений показателей надежности
Укрупненный статистический ряд информации для определения критерия согласия c2
Распределение критерия Колмогорова
Дифференциальная и интегральная функции законов распределения
Закон нормального распределения показателей надежности и его практическое применение
Опытные и теоретические вероятности выхода из строя двигателей
Доверительные границы рассеивания одиночного и среднего значения показателя надежности
Пример расчета доверительных границ одиночного показателя надежности
Абсолютная и относительная предельные ошибки
All Pages

 

Абсолютные характеристики рассеивания показателей надежности - дисперсия и среднее квадратическое отклонение

Рассеивание является важным параметром показателя надежности, позволяющей переходить от общей совокупности к показателям надежности отдельных машин. В инженерной практике эксплуатации машин на основании характеристик рассеивания показателя надежности представляется возможным решать такие важные хозяйственные задачи, как определение сроков постановки отдельных машин на ремонт и стоимости их ремонта, наименьшей и наибольшей наработки на один эксплуатационный отказ и др.

Вследствие рассеивания одиночные значения показателей надежности t_i отклоняются от своего среднего значения на величину t_i-t. Эта разность называется «отклонением», а среднее значение отклонения характеризует величину рассеивания показателя надежности

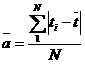, (6)

где N - повторность информации или количество испытанных машин.

Недостатком расчета рассеивания по формуле (6) является необходимость определения абсолютных значений отклонений, что при сложных расчетах может привести к ошибкам.

Более распространенной характеристикой рассеивания при испытании машин на надежность является дисперсия D, которая равна среднему значению квадратов отклонений:

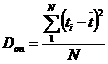, (7)

где - дисперсия, полученная в результате обработки информации по испытанию на надежность относительно небольшого количества машин.

Опытная дисперсия является смещенной по отношению к дисперсии генеральной совокупности этих же машин (т. е. очень большого их количества). Опытная и генеральная D дисперсии связаны между собой соотношением

.

Окончательно получим:

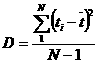. (8)

Пользоваться значением дисперсии не всегда удобно, так как абсолютная величина дисперсии получается, как правило, слишком большой и, кроме того, размерность дисперсии равна квадрату размерности показателя надежности.

В связи с этим наиболее распространенной и удобной для расчетов характеристикой рассеивания является среднее квадратическое отклонение:

. (9)

Как видно из уравнения (9), s значительно меньше по абсолютной величине, чем дисперсия, а его размерность совпадает с размерностью показателя надежности.

Дисперсия D и среднее квадратическое отклонение s являются абсолютными характеристиками рассеивания показателя надежности.

При незначительном количестве информации (N<25) среднее квадратическое отклонение определяется по уравнению:

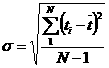. (10)

При наличии статического ряда информации (N > 25) среднее квадратическое отклонение:

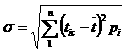. (11)

Определим по выражению (11) среднее квадратическое отклонение доремонтного ресурса двигателя:

=1000 мото-ч.

Расчеты с использованием уравнений (3) и (11) связаны с большим количеством арифметических вычислений и поэтому достаточно трудоемки.

При большом количестве информации (наличие статического ряда) для определения и s может быть рекомендован упрощенный метод расчета – метод сумм. Его сущность заключается в следующем.

Из статистического ряда выписывают две строки: значения середин интервалов и соответствующие им частоты таблица 3.

Таблица 3

Определение коэффициентов а₁, а₂, b₁ и b₂ по методу сумм

Середина интервала, мото-ч	1500	2500	3500	4500	5500	6500	7500	Примечание
Частота mi	2	4	25	28	10	0	1	N = 70
а1 = 39	2	6	31	-	11	1	1	b1 = 13
а2 = 10	2	8	-	-	-	2	1	b2 = 3

К этим строкам приписывают еще две, при этом в третьей строке, примерно на ее середине, делается прочерк одного интервала, а в четвертой строке - три прочерка: средний против прочерка третьей строки и еще два - слева и справа от него.

В третьей строке последовательно складывают частоты от начала строки до прочерка и от конца строки до прочерка. Суммы чисел подсчитывают и обозначают соответственно коэффициентами а₁ и b₁ (см. табл. 3).

В четвертой строке аналогичным образам складывают числовые значения третьей строки. Суммы чисел от начала четвертой строки до первого прочерка и от конца строки до третьего прочерка обозначают соответственно а₂ и b₂.

Среднее значение показателя надежности и среднее квадратическое отклонение определяются по уравнениям:

; (12)

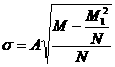, (13)

где А - величина одного интервала; t_{с -} значение середины того интервала, против которого сде­лан прочерк в третьей строке.

.

В нашем расчете:

А=1000 мото-ч;

t_с=4500 мото-ч;

;

;

мото-ч;

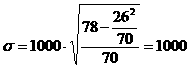мото-ч.

В литературе по теории вероятностей и теории надежности часто для определения среднего значения (математического ожидания) и среднего квадратического отклонения или дисперсии используются понятия начального и центрального моментов.

Для определения моментов статистический ряд информации представляется в виде системы расположенных на одной прямой материальных точек, массой которых является вероятность интервала р_i, а абсциссой - значение показателя надежности в середине этих интервалов t_iс.
Начальным моментом k-го порядка называется сумма произведений всех масс (р_i) на плечи (t_iс) в степени k относительно точки О.

Центральным моментом k-го порядка называется сумма произведений всех масс (р_i) на плечи в степени k относительно точки Ц (см. рис. 2).

В положении, представленном на рис. 2, система материальных точек находится в равновесии. Следовательно, начальный момент первого порядка:

.

Учитывая, что , получим:

.

Таким образом, начальный момент первого порядка равен среднему значению, или математическому ожиданию случайной величины (показателя надежности).

Определим, чему равен центральный момент второго порядка. В соответствии с формулировкой получим:

. (14)

Таким образам, центральный момент второго порядка равен дисперсии, а среднее квадратическое отклонение s — корню квадратному из центрального момента второго порядка

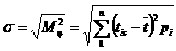. (15)

Кроме указанных основных зависимостей, центральные моменты высшего порядка характеризуют некоторые другие свойства кривых распределения. Так, например, центральный момент третьего порядка характеризует асимметрию кривой, а центральный момент четвертого порядка - эксцесс и т. д.

<< Prev - Next >>