Машиностроение и механика

Article Index
Детали машин: цепные, фрикционные зубчатые передачи
Кинематика цепной передачи
Усилия в ветвях цепи
Расчет цепной передачи на износостойкость
Последовательность расчета цепных передач
Фрикционные передачи
Виды повреждений фрикционных передач
Материалы катков
Цилиндрическая фрикционная передача
Расчет на прочность цилиндрических фрикционных передач с гладкими катками
Последовательность проектного расчета фрикционных передач
Зубчатые передачи
Виды повреждений зубьев и критерии работоспособности зубчатых передач
Цилиндрические зубчатые передачи
Выбор модуля и числа зубьев
Особенности расчета косозубых цилиндрических передач
Многопарность и плавность зацепления
Конические зубчатые передачи
Материалы и термообработка
Допускаемые напряжения изгиба при расчете на усталость
Червячные передачи
КПД червячной передачи
Основные критерии работоспособности и расчета
Материалы и допускаемые напряжения червячных передач
Передача винт-гайка
All Pages

Конические зубчатые передачи

Общие сведения и характеристика. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под углом (рисунок 11.14). Чаще используются передачи с углом = 90°. Конические передачи сложнее цилиндрических в изготовлении и монтаже. Кроме допусков на размеры зубьев, здесь необходимо выдерживать допуски на углы , ₁ и ₂, а при монтаже обеспечивать совпадение вершин делительных конусов. Пересечение осей валов усложняет размещение подшипниковых опор. Одно из конических колес, как правило, шестерня располагается консольно. При такой схеме увеличивается неравномерность распределения нагрузки по длине зуба (рисунок 11.5). В зацеплении конических колес действуют осевые силы. Из опыта эксплуатации установлено, что нагрузочная способность конической прямозубой передачи составляет около 0,85 цилиндрической.

Геометрические параметры. Аналогами делительных днаметров цилиндрических передач в конических являются делительные конусы с углами _1: и ₂. Конусы, образующие которых перпендикулярны образующим делительных конусов (рисунок 11.15), называют дополнительными конусами. Сечение колеса дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения.

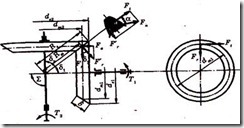
Рисунок 11.14 – Коническая зубчатая передача

Размеры внешнего торцового сечения имеют индекс е, например d_e, R_e и т. д. Размеры в среднем сечении имеют индекс т: d_m, R_m и др. Где R_e – внешнее конусное расстояние, R_m – среднее конусное расстояние, b – длина зуба или ширина зубчатого венца.

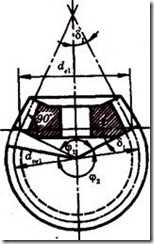
Рисунок 11.15 – Схема приведения прямозубого конического колеса к эквивалентному прямозубому цилиндрическому

Размеры по внешнему торцовому сечению удобнее для измерения, поэтому их указывают на рабочих чертежах. Размеры в среднем торцовом сечении используют при расчетах на прочность. Зависимости размеров в среднем и внешнем торцовом сечениях:

. (11.36)

Передаточное число:

. (11.37)

Выразив d₁ и d₂ через конусное расстояние R и углы делительных конусов и, получим

и при Σ==90° u = tg₂=ctg₁. (11.38)

Эти формулы используют для определения углов и

Силы в зацеплении прямозубой конической передачи. По нормали к поверхности зуба действует нормальная сила F_n, которую раскладывают на окружную силу F_t, радиальную силу F_r и осевую силу F_a. Зависимость между этими силами можно увидеть на рисунке 11.14, где силы приложены к шестерне. Вначале силу F_n раскладывают на F_t и F'_r (см. сечение зуба на рисунке 11.14). Затем F'_r раскладывают на F_а и F_r (на рисунке 11.14 в зоне зацепления). В результате получим следующие зависимости для шестерни

, (11.39)

, ,

,

.

Для колеса силы направлены противоположно. Тогда радиальная сила для колеса равна осевой силе F_a для шестерни (F_r2 = F_a1), а осевая сила для колеса равна радиальной силе F_r для шестерни (F_a2 = F_r1).

Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому. Параметры эквивалентных колес используют в расчетах на прочность. Форма зуба конического колеса в нормальном сечении (внешнее торцевое сечение) дополнительным конусом (рисунок 11.15) такая же, как у цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получается при развертке дополнительного конуса, которая ограничена углом . Тогда диаметры эквивалентных колес можно определить по формулам:

для шестерни

,

для колеса

. (11.40)

Выразив диаметры через z и m, получим , .

Тогда числа зубьев эквивалентных колес можно определить по формулам:

(11.41)

Расчет прямозубой конической передачи на контактную прочность. Для конических колес ρ_пр в формуле (1.4) определяют по радиусам эквивалентных колес. По формулам (11.40), для среднего торцового сечения зуба получим

.

Учитывая связь тригонометрических функций и формулу (11.38), находим

; .

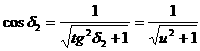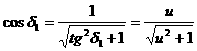После подстановки и преобразований получим

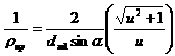. (11.42)

Из формулы (11.42) видно, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоянию от вершины делительного конуса. Удельная нагрузка q также пропорциональна этим расстояниям. Следовательно, отношение постоянно для всех сечений зуба. Постоянными остаются и контактные напряжения по всей длине зуба, это позволяет выполнять расчет в любом сечении, в данном случае по среднему. Удельная нагрузка в этом сечении (рисунок 11.16)

. (11.43)

По сравнению с формулами для прямозубых цилиндрических передач видно, что формулы для q совпадают, а для различаются только числителями: вместо (и + 1).

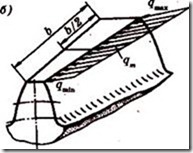
Рисунок 11.16 м Удельная нагрузка сечения:

а) размеры поперечного сечения зуба конического колеса;

б) распределение нагрузки по длине зуба

Учитывая это различие, преобразовываем формулу (11.9) для проверочного расчета прямозубых конических передач в виде

, (11.44)

где – = 0,85 – опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической.

Для проектного расчета формулу (11.44) преобразуют. Считают, что основными габаритными размерами для конических передач являются d_e2 и R_e, а нагрузка является моментом Т₂ на ведомом валу. После введения этих параметров и некоторых преобразований получают

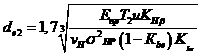, (11.45)

где – коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. Рекомендуют К_be < 0,З. Чаще принимают значение К_be = 0,285. Тогда

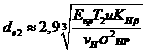. (11.46)

В формулах (11.45) и (11.46) принято: = 20°, K_Hv= 1,5. Коэффициент полезного действия. КПД зубчатой передачи

, (11.47)

где Р₁, – мощность на входе, Р₂ – мощность на выходе, Р_r – мощность, потерянная в передаче.

При этом, Р_r = Р₃ + Р_п +(–Р_Г), где Р₃ – мощность, потерянная на трение, Р_п – мощность, потерянная на трение в подшипниках, Р_г – мощность, потерянная на разбрызгивание и перемешивание масла (гидравлические потери).

КПД зубчатой передачи можно записать в виде

, (11.48)

где ₃ – КПД зацепления, _п – КПД пары подшипников, _г – КПД гидравлических потерь.

На практике определяют суммарные потери в передаче. В расчетах можно использовать следующие ориентировочные значения КПД одной ступени зубчатого редуктора на подшипниках качения при номинальной нагрузке: