Машиностроение и механика

Особенности расчета косозубых цилиндрических передач

Геометрические параметры. У косозубых колес зубья располагаются под некоторым углом к образующей делительного цилиндра (рисунок 11.9). Оси колес остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного профиля, как и для нарезания прямых. Поэтому контур косого зуба в нормальном сечении n – n совпадает с контуром прямого зуба. Модуль в этом сечении является стандартным

Рисунок 11.9 – Схема косозубой цилиндрической передачи (геометрические размеры)

В торцовом сечении t—t параметры косого зуба изменяются в зависимости от величины угла р:

Окружной шаг .

Окружной модуль .

Делительный диаметр .

Индекс n приписывают параметрам в нормальном сечении, а индекс t приписывают параметрам в торцовом сечении.

Принято считать, что прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении определяют через параметры эквивалентного прямозубого колеса (рис. 11.10).

Нормальное к зубу сечение образует эллипс с полуосями

с=r и е=, где . В зацеплении находятся зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии . Радиус кривизны эллипса на малой оси (см. геометрию) .

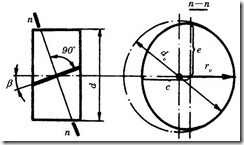
Рисунок 11.10 – Схема для определения эквивалентных параметров косозубых цилиндрических передач

В соответствии с этим форма косого зуба в нормальном сечении эквивалентна прямозубому колесу, диаметр которого

(11.20)

и число зубьев

или

. (11.21)

Увеличение эквивалентных параметров (d_v и z_v) с увеличением угла повышает прочность косозубых передач.