Машиностроение и механика

Article Index
Детали машин: цепные, фрикционные зубчатые передачи
Кинематика цепной передачи
Усилия в ветвях цепи
Расчет цепной передачи на износостойкость
Последовательность расчета цепных передач
Фрикционные передачи
Виды повреждений фрикционных передач
Материалы катков
Цилиндрическая фрикционная передача
Расчет на прочность цилиндрических фрикционных передач с гладкими катками
Последовательность проектного расчета фрикционных передач
Зубчатые передачи
Виды повреждений зубьев и критерии работоспособности зубчатых передач
Цилиндрические зубчатые передачи
Выбор модуля и числа зубьев
Особенности расчета косозубых цилиндрических передач
Многопарность и плавность зацепления
Конические зубчатые передачи
Материалы и термообработка
Допускаемые напряжения изгиба при расчете на усталость
Червячные передачи
КПД червячной передачи
Основные критерии работоспособности и расчета
Материалы и допускаемые напряжения червячных передач
Передача винт-гайка
All Pages

Многопарность и плавность зацепления. В отличие от прямых, косые зубья входят в зацепление не сразу по всей длине, а постепенно. Зацепление перемещается в направлении от точек 1 к точкам 2 (рисунок 11.9).

Расположение контактных линий в поле косозубого зацепления показано на рисунке 11.11, а, б (сравни с рисунком 11.3 – прямозубое зацепление). При движении линии контакта перемещаются в поле зацепления в направлении, показанном стрелкой. В рассматриваемый момент времени в зацеплении находится три пары зубьев 1, 2 и 3. Пара 2 находится в зацеплении по всей длине зубьев, а пары 1 и 3 – лишь частично. Затем пара 3 выходит из зацепления и перемещается в положение 3', а в зацеплении еще остались две пары 2' и 1’. В отличие от прямозубого косозубое зацепление не имеет зоны однопарного зацепления. В прямозубом зацеплении нагрузка с двух зубьев на один или с одного на два передается мгновенно.

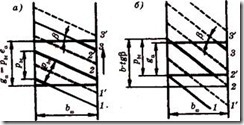
Рисунок 11.11 – Многопарность косозубого цилиндрического зацепления

Это сопровождается ударами и шумом. В косозубых передачах зубья нагружаются постепенно по мере захода в поле зацепления, а в зацеплении всегда находится минимум две пары зубьев. Плавность косозубого зацепления значительно уменьшает шум и динамические нагрузки.

Косозубые колеса могут работать без нарушения зацепления даже при коэффициенте торцевого перекрытия < 1, если обеспечено осевое перекрытие b_w >; (рисунок 11.11, б). Отношение

(11.22)

называют коэффициентом осевого перекрытия. Рекомендуется принимать ≥ 1,1. В косозубом зацеплении нагрузка распределяется на всю суммарную длину контактных линий 1, 2, 3. Удельная нагрузка уменьшается с увеличением суммарной длины контактных линий Из рисунка 11.11 можно установить, что при , равному целому числу,

(11.23)

и не изменяется при движении, так как уменьшению линии 3 всегда соответствует равное увеличение линии 1. Из формулы 11.23 видно, что растет с увеличением , что выгодно. Однако при увеличении увеличиваются осевые нагрузки в зацеплении (см. далее), поэтому рекомендуют принимать = 8 – 20°.

На боковой поверхности косого зуба линия контакта располагается под некоторым углом (рисунок 11.12, а). Угол , увеличивается с увеличением . По линии контакта нагрузка распределяется неравномерно. Ее максимум на средней линии зуба, так как при зацеплении серединами, зубья обладают максимальной суммарной жесткостью.

При движении зуба в плоскости зацепления линия контакта перемещается в направлении от 1 к 3 (рисунок 11.12, б), при этом опасным для прочности может оказаться положение 1, в котором у зуба отламывается угол. Трещина усталости образуется у корня зуба в месте концентрации напряжений и затем распространяется под некоторым углом. Вероятность косого излома отражается на прочность зубьев по напряжениям изгиба, а концентрация нагрузки q – на прочность по контактным напряжениям.

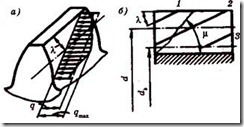
Рисунок 11.12 – Расположение линии контакта на боковой поверхности

Силы в зацеплении. В косозубой передаче (рисунок 11.13) нормальную силу F_n раскладывают на три составляющие:

Рисунок 11.13 – Силы в зацеплении косозубой цилиндрической передачи

окружную силу ,

осевую силу , (11.24)

радиальную силу .

Тогда нормальная сила .

Осевая сила в зацеплении дополнительно нагружает опоры валов, что является недостатком косозубых колес.

Расчет зубьев по контактным напряжениям. Для косозубых колес удельная нагрузка с учетом формул (11.23) и (11.24)

, (11.25)

где К_нα – коэффициент неравномерности нагрузки одновременно зацепляющихся пар зубьев.

Заменяя в формуле (11.8) значение d_w1 на диаметр эквивалентного колеса d_vl [см. формулу (11.20)], получаем

. (11.26)

Сравнивая отношения в формуле (1.4) для прямозубых (формулы 11.6 и 11.8) и косозубых колес, определяем

или

. (11.27)

Обозначим

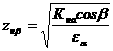, (11.28)

где Z_Hβ – коэффициент повышения прочности косозубых передач по контактным напряжениям. Используя формулу (11.9) получим для косозубых передач

. (11.29)

В косозубых передачах, из–за ошибок при нарезании зубьев, может быть частично нарушено двухпарное зацепление. Это приводит к тому, что одна пара зубьев нагружается больше чем другая, поэтому коэффициент К_Нα учитывает неравномерность нагрузки. При этом различают К_Нα для расчетов по контактным напряжениям и K_Fα для расчетов по напряжениям изгиба. Значения коэффициентов выбирают по рекомендациям из справочников в зависимости от окружной скорости в зацеплении и степени точности изготовления. При проектном расчете эта информация не известна, поэтому значение Z_H в формуле (11.29) определяют приближенно. Принимая средние значения = 12°, = 1,5 и К_Нα= 1, 1, получаем Z_нβ =0,85, а формулы (11. 10) и (11. 12) проектного расчета путем умножения числовых коэффициентов на для косозубых передач будут иметь вид

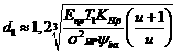, (11.30)

. (11.31)

Расчет зубьев по напряжениям изгиба. Расчет выполняют с учетом увеличения прочности косозубых передач по сравнению с прямозубыми. Тогда формулы (11.18) и (11.19) для косозубых передач будут иметь вид: для проверочного расчета,

(11.32)

для проектного расчета (принимая приближенно К_Fn = 1)

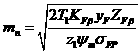, (11.33)

где Z_Fβ – коэффициент повышения прочности косозубых передач по напряжениям изгиба:

, (11.34)

где _а – коэффициент перекрытия учитывающий уменьшение нагрузки ввиду многопарности зацепления. Его определяют по формуле:

. (11.35)

Знак «+» – для внешнего, а «–» – для внутреннего зацепления.

K_Fa – коэффициент неравномерности распределения нагрузки одновременно зацепляющихся пар зубьев (выбирают по справочникам), – коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии к основанию зуба.

Коэффициент формы зуба y_F выбирают по справочникам в зависимости от эквивалентного числа зубьев z_v. Значения z_{1 , m} и выбирают по справочникам.