Машиностроение и механика

Цилиндрические зубчатые передачи

Расчет прямозубых цилиндрических передач на прочность

Расчет прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354-87. Рассмотрим основы расчета с некоторыми упрощениями.

Силы в зацеплении. На рисунке 11.6 F_n – нормальная сила действующая по линии зацепления к рабочим поверхностям зубьев. Переносим силу F_n в полюс зацепления и раскладываем на окружную силу F_t и радиальную силу F_r. Такая расчетная схема используется для расчета валов и опор. При известном Т₁ можно записать

, (11.4)

далее через нее выражают остальные составляющие:

(11.5)

Расчет зубьев на контактную прочность. Наименьшей контактной усталостной прочностью обладает околополюсная зона, где наблюдается однопарное зацепление (рисунок 11.3).

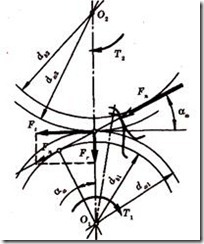
Рисунок 11.6 – Силы, действующие в прямозубом цилиндрическом зацеплении

Рисунок 11.7 – Схема к расчету прочности зубьев по контактным напряжениям

Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления (рисунок 11.7). Контакт зубьев рассматривают как контакт двух цилиндров с радиусами ρ₁ и ρ₂. Контактные напряжения определяют по формуле (1.4)

.

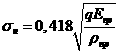Для прямозубых передач с учетом формул (11.3) – (11. 5)

. (11.6)

Радиусы кривизны эвольвент зубьев в зоне контакта

. (11.7)

Тогда

, (11.8)

где , знак «+» – для наружного, а «–» – для внутреннего зацепления.

Подставляя полученные выражения (11.6)и(11.8)в формулу (1.4) и заменяя получаем

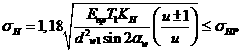. (11.9)

Параметр u = называют передаточным числом.

Значения расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из пары колес, у которого меньше допускаемое напряжение _нр.

Формулу (11.9) используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете требуется определить размеры передачи по заданным условиям: крутящему моменту Т₁ или Т₂ и передаточному числу и. Для этого формулу (11.9) решают относительно d₁ или а. Неизвестные параметры выбирают по рекомендациям из справочников. В нашем случае принимаем d_w1 = d₁; = = 20° (sin2 = 0,64), K_Hv = 1,15 (этот коэффициент зависит от окружной скорости и, которая пока не известна, поэтому принято некоторое среднее значение). Из составляющих коэффициента К_н [см. формулу (11.3)] остается К_нβ.. Вводим новое обозначение – коэффициент ширины шестерни относительно делительного диаметра. Подставляя принятые значения в формулу (11.9) и решая относительно d₁, получаем

. (11.10)

Решая относительно межосевого расстояния а, заменяем : и вводим – коэффициент ширины колеса относительно межосевого расстояния. После преобразований с учетом зависимости

(11.11)

получим

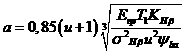. (11.12)

При расчетах цилиндрических зубчатых передач чаще используют формулу (11.12), так как габариты передачи определяет межосевое расстояние. Значения Ки выбирают по рекомендациям из справочников.