Зубчатые передачи
Геометрический расчет эвольвентных прямозубых цилиндрических передач
Рассмотрим сечение цилиндрического зубчатого колеса с внешними зубьями плоскостью, перпендикулярной к оси колеса (главное, или торцовое сечение). Выделяют окружность вершин зубьев (
) и окружность впадин (
), между которыми заключен зуб колеса. Высота зуба 
Эвольвентный профиль и окружность впадин соединяются переходной кривой. Общая точка L эвольвенты и переходной кривой называется граничной точкой профиля.
Расстояние между одноименными профилями двух соседних зубьев, измеренное по дуге окружности, называется окружным шагом зубьев. Для окружности произвольного радиуса 
где Py – окружной шаг;
Sy – окружная толщина зуба;
ey – окружная ширина впадины.
Длину окружности можно выразить через шаг Py и число зубьев Z:
откуда
где 
– окружной модуль.
Модуль и шаг зависят от окружности, к которой они относятся.
На колесе выделяется расчетная окружность, на которой шаг и модуль зубьев равны шагу и модулю зуборезного инструмента. Эта окружность называется делительной (r, d), а модуль зубьев на делительной окружности называется расчетным модулем зубчатого колеса:
(1.1)
где P – шаг по делительной окружности (делительный шаг). Значения m регламентированы СТ СЭВ 310-76, ГОСТ 9563-80.
1 ряд– 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5 и т.д.
2 ряд– 0,9; 1,125; 1,375; 1,75; 2,25; 2,75 и т.д.
Диаметр делительной окружности
(1.2)
Центральный угол 
называется угловым шагом зубьев.
(1.3)
В основе зуборезного инструмента, используемого для нарезания эвольвентных цилиндрических колес по методу обкатки, лежит исходный производящий контур, под которым понимается контур
зубьев зуборезной рейки в сечении плоскостью, перпендикулярной к направлению ее зубьев. Параметры этого контура стандартизованы (СТ СЭВ 308-76 для 
), ГОСТ 13755-81 (рис. 1.2).
Высота зуба исходного производящего контура
(1.4)
где 
– коэффициент высоты головки зуба;
– коэффициент радиального зазора.
Угол α = 20° называется углом главного профиля.
Прямая, по которой толщина зуба равна ширине впадины, называется делительной. Зубчатые колеса бывают: 1) без смещения исходного контура (некорригированные); 2) со смещением.
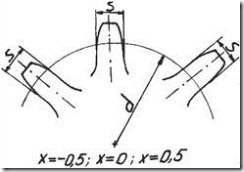Если делительная прямая исходного производящего контура касается делительной окружности нарезаемого колеса, то нарезается колесо без смещения, в противном случае нарезается колесо со смещением (рис . 1.3).
В зависимости от коэффициентов смещения зацепляющихся колес различают следующие типы передач: 1)передача без смещения (X1 = X2 = 0); 2)равносмещенная передача (X1 = -X2 ≠ 0, Х∑ = X1 + X2 =0); 3) положительная передача (X∑ > 0); 4) отрицательная передача (X∑ < 0). В передачах без смещения и равносмещенных[1]
(угол зацепления равен углу главного профиля), 
(делительные окружности одновременно являются и начальными), высота зуба h = 2,25m. В передачах без смещения
(1.5)
(1.6)
Межосевые расстояния для стандартных редукторов стандартны:
= 40; 50; 63; 80; 100; 125; 160; 180; 200; 225; 250; 280; 315 и т.д.
При нарезании зубьев без смещения можно изготовить колесо лишь с Z1min≥17 (если X∑ >0, то Z1min = 12).
При окружных скоростях колес
, Z1 и Z2 принимают кратными друг другу;
, Z1 и Z2 принимают взаимно простые числа зубьев.
Расчет геометрических параметров цилиндрических зубчатых передач выполняется по ГОСТ 16530-83.