Тепловая работа аппарата с частичным теплообменом
1. Рассмотрим аппарат идеального вытеснения, в котором идет экзотермическая реакция.
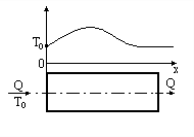Qi – тепловой эффект реакции.
ri – скорость химической реак-ции.
Предполагаем, что в аппарате происходит экзотермический эффект, тогда:
1 – количество тепла, выделившегося в единицу времени;
2 – количество тепла, теряемое с поверхности аппарата во внешнюю среду;
ρ – плотность вещества в потоке;
СT – теплоёмкость вещества в потоке;
k – коэффициент теплопередачи от потока вещества к внешней среде;
f – удельная поверхность теплопередачи, отношение поверхности аппарата к его объёму;
Т0 – начальная температура на входе в аппарат;
Т – текущее значение температуры в произвольный момент времени;
Тс – температура среды;
t – время пребывания вещества в аппарате.
Приход тепла в тепловом балансе такого аппарата является суммой физического тепла вещества, поступающего в аппарат с потоком, и тепла, выделяющегося в ходе химической реакции. Расход тепла обусловлен уносом тепла веществом, покидающим аппарат с выходным потоком и потерями в окружающую среду.
Физическое тепло вещества на входе и выходе аппарата определяется его температурой, теплоемкостью и массой. Потери тепла пропорциональны разности температур в аппарате и температуры окружающей среды, а также поверхности теплообмена. Количество выделяющегося тепла зависит от теплового эффекта реакции и пропорционально скорости реакции.
Решение дифференциального уравнения теплового баланса дает функцию изменения температуры от времени пребывания вещества в аппарате. Поскольку время пребывания пропорционально расстоянию от точки входа в аппарат до произвольной точки внутри аппарата, для которой мы определяем значение температуры, можно построить профиль изменения температуры внутри аппарата.
В случае экзотермической химической реакции температура по длине аппарата изменяется от начального значения T0 (в точке входа в аппарат), которое определяется из начальных условий для решения дифференциального уравнения теплового баланса, затем возрастает до некоторого максимума, после чего убывает.
Рост температуры объясняется тем, что количество тепла, выделяющегося в начальный момент реакции, превышает возможности теплообмена с внешней средой. Избыток тепла приводит к увеличению температуры вещества в аппарате.
Скорость химической реакции в начальный момент высока, но поскольку со временем концентрация исходных веществ уменьшается (расходуются исходные вещества), количество тепла, выделяющегося за счет химической реакции в единицу времени также падает. Когда количество выделяющегося и отводимого тепла становится одинаковым, устанавливается максимальная температура в некоторой точке аппарата.
Далее количество выделяющегося тепла становится меньше, чем отводимого. Дефицит тепла в балансе приводит к снижению температуры вещества. На профиле температур в аппарате это отображается падающим участком.
На практике моделирование аппарата с частичным теплообменом такого типа позволяет проверить, не превысит ли максимальная температура допустимых значений. В таком случае необходимо изменить условия теплообмена в критической зоне аппарата, например использовать принудительное охлаждение или жидкостное охлаждение, что позволит увеличить коэффициент теплопередачи от вещества в аппарате к окружающей среде и количество отводимого тепла.
2. Работа аппарата с экзотермической химической реакцией в режиме идеального перемешивания.
Имеем химическую реакцию с выделением тепла. Количество тепла в единицу времени пропорционально скорости химической реакции:
– количество тепла, поступающего с входящим потоком;
– количество тепла, выносимое из аппарата выходящим потоком;
– количество тепла, выделяющегося в ходе химической реакции;
– количество тепла, теряющегося в поверхности аппарата.
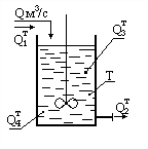
Если известны скорость химической реакции и тепловой эффект, то мы считаем всю величину Q3 известной; Q1 тоже известна; Q2 нельзя считать известной (мы не знаем Т); Q4 тоже неизвестна.
Решением этого уравнения теплового баланса является значение температуры внутри реактора. В результате моделирования мы определяем такую температуру, в зависимости от скорости химической реакции, идущей внутри аппарата. Путём итерационного расчёта значение температуры в реакторе уточняется.
Расчёт температуры позволяет судить о том, как в тепловом отношении будет работать аппарат при заданных условиях, при заданном составе вещества на входе, при заданной производительности, при заданной начальной температуре и геометрических размерах аппарата. На основании таких расчётов можно делать вывод, может ли процесс осуществляться автогенно, требуется ли дополнительный отвод тепла или необходим дополнительный источник тепла (топливо, электроэнергия и др.).
Мы познакомились с моделированием объектов на простейшем молекулярном уровне. Реальные модели процессов и объектов металлургии, как правило, значительно сложнее, они включают в себя элементы описания на более высоких уровнях: малого объема, рабочей зоны аппарата и т.д. Лишь в некоторых частных случаях можно результаты моделирования на молекулярном уровне распространить на уровень технологического аппарата в целом. Так, если химические реакции идут гомогенно, а технологический объект является аппаратом идеального перемешивания, не требуется его описания на уровне малого объема и рабочей зоны. В этом случае мы можем рассматривать аппарат в целом, как некую материальную точку в физике, поскольку, например концентрации и температуры в разных точках внутри аппарата одинаковы.
Создание модели реального процесса или технологического аппарата требует усилий, как правило, коллектива специалистов. Тем не менее, главная роль в коллективе на этапе постановки задач, на этапе получения выводов и их трактовки принадлежит к специалисту предметной области – инженеру-металлургу. Только инженер-металлург может определять такие элементы, которые могут относиться к существенным сторонам модели.
Построение математической модели технологического объекта позволяет в пределах имеющихся знаний уточнить закономерности, управляющие работой объекта. В этом смысле модель является инструментом научного познания, позволяя совершенствовать теоретические знания об объекте.
Полученная модель технологических процессов и объектов представляет собой инструмент, позволяющий прогнозировать поведение моделируемых объектов. Под прогнозированием следует понимать возможность расчета выходных характеристик технологического объекта (состава, массы полученного продукта в частности) от известных значений фиксированных входных характеристик и выбранных величин управляющих воздействий.
В таком виде модель представляет инструмент для управления технологическим объектом, позволяя ответить на вопрос: какие величины управляющих воздействий следует выбрать (и поддерживать) для того, чтобы выходные характеристики технологического объекта приняли желаемые значения.
Главное назначение модели – она предоставляет необходимые инструменты для оптимизации.