Моделирование процессов и объектов в металлургии
СИСТЕМНЫЙ АНАЛИЗ
Основным понятием данного раздела является понятие о технологических процессах и объектах как о системах.
Система – составной объект, части которого закономерно объединены и совместно выполняют общую функцию.
Системы могут быть искусственными и естественными.
Естественные системы. Они не имеют определенной цели существования и создаются в ходе эволюции. Примером естественных систем являются биологические, например организмы. Другим примером являются социальные системы.
Искусственные системы отличаются тем, что они создаются для вполне определенной цели (технические и технологические системы).
 Целью технологических систем в металлургии цветных металлов является переработка сырья, содержащего цветные металлы, с получением продукта, имеющего заданные свойства.
Целью технологических систем в металлургии цветных металлов является переработка сырья, содержащего цветные металлы, с получением продукта, имеющего заданные свойства.
Система, как целостный объект, существует во внешней по отношению к ней среде (можно провести границу между системой и внешней средой). В технологических системах внешняя среда проявляет себя, как источник перерабатываемого сырья и как потребитель произведенного продукта.
В технологических системах внешняя среда проявляет себя, как источник перерабатываемого сырья и как потребитель произведенного продукта.
Система мысленно или физически может быть разделена на элементы, таким образом система представляет собой совокупность элементов. Элементы объединяются в систему за счет связей. Таким образом, в любой системе существует определённая структура связей.
Задачей системного анализа является определение свойств изучаемой системы. Изучение этих свойств позволяет в последующем выбрать соответствующий задаче метод построения модели. Таким образом, системный анализ является инструментом, позволяющим изучать функционирование сложных технологических систем и выбирать методы моделирования таких систем.
Система – это объект, обладающий набором системных свойств, к числу которых относятся:
1. Целостность и членимость;
2. Наличие существенных связей;
3. Наличие структуры или организации;
4. Наличие интегративного качества.
1. Целостность и членимость. Система, как целостный объект, может быть выделена из внешней среды, а как составной объект, может быть мысленно или физически разделена на составные части. Границами технологической системы в металлургии являются точки поступления исходного сырья и выхода готовой продукции. Масштаб системы может быть различным: от предприятия до отдельно рассматриваемой химической реакции, которая протекает в том или ином технологическом процессе. Как систему можно рассматривать также и отдельный технологический аппарат, совокупность таких аппаратов или технологических операций, т.е. технологическую схему, участок, отделение или цех.
2. Наличие существенных связей. Элементы объединяются в систему за счет связей между элементами. Связи можно разбить на три основные группы:
а) вещественные;
б)энергетические;
в)информационные.
Вещественные связи – представляют собой потоки вещества, циркулирующие между элементами системы. Особенности потоков вещества:
· агрегатное состояние может быть различным (твердое, жидкость, газ);
· фазовое состояние (одно- или многофазное).
Вещественные связи в системе подчиняются закону сохранения вещества: сумма масс всех потоков, поступающих в элемент системы, равна сумме масс, покидающих элемент системы. То есть для каждого элемента системы мы можем составить материальный баланс.
Энергетические связи – представляют собой потоки энергии, циркулирующие между элементами системы. Для металлургических систем виды энергии могут быть различными, наибольшее значение имеют потоки тепловой энергии. В некоторых технологических процессах (электролизе, например) более важное значение имеют и другие виды энергии (электрическая, механическая).
Энергетические связи подчиняются закону сохранения энергии, таким образом, для каждого элемента системы можно составить энергетический (в частности тепловой) баланс.
Информационные связи – представляют собой потоки информации, циркулирующие между элементами системы. Информация, циркулирующая в потоках, представляет собой величины технологических параметров, которые характеризуют работу каждого элемента системы. Чем выше уровень технологии, тем больше количество таких параметров измеряется по ходу технологического процесса, тем большее количество информации получается в информационном потоке. В отличие от вещественных и энергетических связей, информационные потоки описываются не законами сохранения, а законами распространения информации.
Все связи системы характеризуются направленностью.
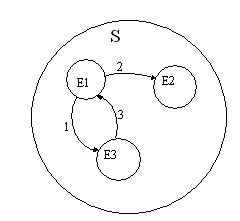
Е1…Е3 – элементы 1…3.
Связь 1 является прямой связью Е1 и Е3, связь 3 является обратной.
Связи могут быть физически наполненными и не наполненными.
Физически не наполненные связи – это связи типа отношений: А>В
A<B
A=B.
Физически наполненные – связи вещественные и энергетические.
Связи должны обладать устойчивостью, то есть они должны существовать достаточно длительно во времени.
Вещественные связи в технологических системах представляют собой системы промышленного транспорта. Конкретный вид этих систем зависит от свойств вещественной связи: для твердых материалов – механические транспортирующие машины- конвейеры различных типов. Для жидкостей и газов используют системы трубопроводного транспорта.
Связи в системе должны быть существенными. Существенность оценивается количественно по величине силы связи – это отношение потока вещества (энергии), проходящего через эту связь к общему потоку вещества (энергии) в системе:
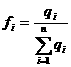
где: qi – доля общего потока вещества (энергии), приходящаяся на i связь;
![]() - общий поток вещества (энергии) в системе.
- общий поток вещества (энергии) в системе.
В том случае, если сила связи больше критерия значимости α – связь существенная (α = 0,02…0,05). Величина критерия значимости выбирается исходя из ошибок измерения технологических параметров в том или ином технологическом процессе.
Наличие структуры или организации
Устойчивая во времени конфигурация связей образует структуру системы.
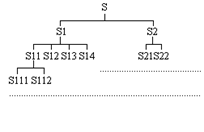
При описании систем на стадии системного анализа используется иерархический подход: на первом этапе описания системы стремятся представить её как совокупность небольшого количества элементов, при этом каждый элемент представляет собой подсистему и на следующем иерархическом уровне может быть разделен на некоторое количество своих элементов.
Иерархический подход позволяет представить сложные технические системы в простом виде, упрощая понимание взаимодействия всех элементов, что дает возможность представить функционирование всей системы в целом. Чем глубже уровень описания системы, тем больше элементов мы различаем в ее составе.
Например, автомобиль можно рассматривать как техническую систему. Цель такой системы – перевозка пассажиров и/или груза в заданном направлении (по дороге) за счет использования энергии топлива. На первом этапе системного анализа автомобиль является совокупностью небольшого числа элементов: двигатель является источником энергии, ходовая часть обеспечивает передвижение по дороге, рулевое управление и тормоза обеспечивают следование заданной траектории движения, кузов, шасси и кабина объединяют все элементы и несут груз и пассажиров.
При более глубоком анализе, на следующем иерархическом уровне, каждый из перечисленных элементов автомобиля рассматривается как подсистема, состоящая из своих элементов. Двигатель как источник энергии для движения, преобразует химическую энергию топлива в механическую энергию вращения вала. Для этого двигатель должен иметь систему питания топливом и воздухом (без воздуха топливо не горит), систему выпуска отработавших газов, механизм распределения топливо-воздушной смеси по цилиндрам, кривошипно-шатунный механизм, с помощью которого движение поршней в цилиндрах преобразуется во вращение вала.
Такой анализ можно продолжать и далее, до отдельных деталей, из которых вес и состоит. Разумеется, количество таких деталей будет возрастать очень быстро и достигнет многих тысяч. Если начать с того, что автомобиль является совокупностью нескольких тысяч деталей, то взаимодействие их понять невозможно.
Существуют типовые структуры связей в системах:
1.Сетевая структура. Пусть имеется система из пяти элементов, число элементов n=5, каждый из них имеет n – 1 связь.

Каждый элемент в такой структуре связан со всеми остальными.
Достоинства: устойчивость, равноправность элементов. В случае, если какой-либо элемент неработоспособен (потерял связи с остальными элементами системы), система в целом остается работоспособной. Ущерб с точки зрения функционирования системы минимальный и одинаковый для любого из элементов.
Количество связей в такой структуре наибольшее, а каждая связь требует определенных затрат. Следовательно, такая структура надежная, но дорогая. Ее применение оправданно там, где надежность функционирования системы является основным требованием, например в энергетике.
2. Скелетная структура. Рассмотрим систему из девяти элементов, n=9. Пусть система имеет скелетную структуру. Каковы ее особенности?

Такая структура обладает компромиссными качествами и требованиями к элементам. Связи элементов образуют фрагменты, которые объединяются затем в целостную систему. Требования в отношении надежности функционирования элементов становятся неодинаковыми. Так например, нарушения в работе элемента 3 означают минимальный ущерб для системы, означающий потерю только одного этого элемента. Если же перестает работать элемент 1, то система теряет целый фрагмент, а нарушение работы элемента 4 означают, что система распадается на отдельные фрагменты и перестает функционировать. Очевидно, что самые высокие требования по надежности предъявляются к элементу 4, средние – к элементам 1 и 7, минимальные- к элементам 3,6 и 9.
3. Централистская структура. Рассмотрим еще раз систему из девяти элементов, n=9, но имеющую централистскую структуру. Основное ее отличие от предыдущих структур в том, что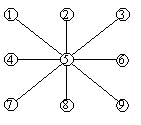
количество связей минимально. Это способствует снижению стоимости связей, но выдвигает жесткие требования к надежности элементов. Наиболее надежным должен быть центральный элемент системы, поскольку при невозможности его функционирования система тут же превращается в набор разрозненных элементов, т.е. перестает работать как целостный объект. К периферическим элементам требования по надежности остаются достаточно низкими: утрата любого из этих элементов приводит к минимальному ущербу для функционирования всей системы. Пример такой системы в технике – стационарные телефонные системы связи.
Наличие интегративного качества
Интегративное качество – это новое качество системы, которым обладает вся система в целом и не обладает ни один отдельно взятый элемент системы. Возникновение интегративного качества рассмотрим на следующем примере.

Медеплавильный завод как технологическая система имеет ясно поставленную цель: он создан для переработки медных концентратов и получения черновой меди. Пользуясь методом системного подхода, мы можем выделить в структуре медеплавильного завода несколько (три, например) основных элемента. Такими элементами пусть будут цех подготовки шихты, плавильное отделение, в котором из приготовленной шихты получают медный штейн, и отделение конвертирования, где штейн перерабатывается на черновую медь.
Ни один из трех элементов системы не может решить поставленной задачи: цех подготовки шихты перерабатывает медные концентраты, но производит не черновую медь, а только готовит шихту для последующей плавки на штейн. Отделение конвертирования производит черновую медь, но не из медных концентратов, а из ранее полученного штейна, а плавильное отделение и вовсе далеко от поставленной цели, поскольку для его работы необходима подготовленная шихта, а результатом плавки является всего лишь полупродукт – медный штейн.
Интегративное качество образуется только в совокупности всех элементов системы. В целом медеплавильный завод решает поставленную задачу, хотя ни один из его элементов не обладает таким свойством.
Внешние связи системы
Рассмотрим технологическую систему, находящуюся в контакте с внешней средой. Что же понимать под внешней средой? По отношению к технологической системе внешняя среда - это источник сырья и потребитель полученного продукта.
Руководствуясь этим понятием легко определить границы рассматриваемой технологической системы, т.е. выделить ее из внешней среды. Масштаб системы при этом может быть различным. Металлургическое предприятие является примером системы большого масштаба, цех предприятия, участок и отделение- системы меньшего масштаба, еще меньший масштаб представляет собой отдельно взятый технологический аппарат или операция технологической схемы. Наименьший масштаб технологических систем в металлургии цветных металлов соответствует физико-химическому явлению: химической реакции, которая сопровождается тепло- и массообменном.
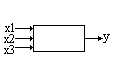
В процессе выделения системы из внешней среды мы должны определить внешние связи. Связи эти направленные, часть из них ведет от внешней среды к системе и называется входами системы, другие связи называются выходами и ведут от системы к внешней среде. Входы и выходы системы объединяют в несколько основных групп.

Х – вектор фиксированных входных характеристик (X=х1,х2,х3,…,хn) – набор из n величин, характеризующих вход системы. Компоненты вектора х известны нам по величине, но недоступны для изменения (например, состав сырья по определяемым компонентам, габариты печи и др.).
U – вектор управляющих воздействий. (U=u1,u2,…um). Число компонентов вектора U и Х может быть в общем случае разным. Компоненты этого вектора так же известны нам по величине и доступны для изменения в определенных пределах: a1≤U1≤ b1; a2≤U2≤b2; am≤Um≤bm (например, температура процесса, давление процесса и др.). Компоненты вектора управляющих воздействий являются своего рода «рулями», изменяя которые в разрешенных пределах мы добиваемся хода технологического процесса в нужном для нас направлении, т.е. осуществляем управление процессом.
V – вектор возмущений. Компоненты этого вектора не известны нам по величине (отсутствуют средства измерений, методики анализа, отсутствует перечень величин), т.е. это неконтролируемый вектор. В реальных технологических системах возмущения проявляются всегда. В некоторых частных случаях при анализе систем ими можно пренебречь.
Y – вектор выходных характеристик (Y=y1,y2,y3,…уk). Компоненты этого вектора известны нам по величине; влиять на эти величины непосредственно мы не можем. Однако, изменяя доступные нам входы системы U, мы влияем на выход Y. Это влияние можно отобразить такой символической надписью:
Y = Ф(X, U, V, τ)
– выход зависит от всех входов системы и момента времени.
В общем случае, выход системы зависит от состояния её входов и момента времени, в который мы определяем состояние выхода.
Компоненты вектора Y – это состав и масса полученных технологических продуктов.
Управление технологической системой означает выбирать и поддерживать такие величины управляющих воздействий u1…um, которые:
· не нарушают ограничений;
· позволяют получить необходимое значение y1…yk на выходе.
Символ Ф называется оператором перехода. Если он сформулирован математически, то это означает, что построена математическая модель процесса. В простейшем случае Ф может быть задан аналитическим выражением, аргументами которого являются входные величины и время.
В большинстве случаев для Ф нет аналитических выражений, но существует определённый алгоритм, действуя в соответствии с которым можно рассчитать значение компонентов y1…yx по известным нам входным характеристикам и управляющим воздействиям. Другими словами, зная Ф (имея математическую модель технологического объекта), мы можем рассчитать (предсказать, прогнозировать) состояние выхода этого объекта в зависимости от состояния входов для любого момента времени. Для этого «всего лишь» необходимо установить конкретную форму оператора перехода Ф, т.е. построить математическую модель. Как же это делается?
Классификация систем по их свойствам
Выбор метода построения модели представляет собой сложную задачу, включающую элементы творческого процесса и трудно поддающуюся формализации. Вряд ли возможно придумать некий алгоритм, следуя которому мы для любой системы тут же получим ее модель. В некотором смысле моделирование сочетает научный подход с искусством. В качестве наиболее общей рекомендации следует отметить, что выбор метода построения математической модели объекта в большой степени зависит от свойств самого объекта, т.е. технологической системы. Поэтому предварительно надо познакомиться с классификацией систем.
Для классификации систем используется несколько признаков:
а) число элементов и подсистем;
б)характер связи с внешней средой;
в) зависимость характеристик систем от времени;
г) тип входных и выходных величин;
д) уровень организации системы и задачам.
Число элементов и подсистем. По этому признаку различают простые (малые) системы, содержащие меньше 1000 элементов, и большие или сложные системы с числом элементов более 1000. Число элементов сильно зависит от уровня детализации при описании систем, поэтому любая система при повышении уровня этой детализации склонна оказаться в числе больших. На практике к классу больших систем могут быть отнесены предприятия и их объединения, большие цеха, в составе которых несколько переделов или отделений, сложные многостадийные технологические схемы. Отдельный технологический аппарат скорее будет простой или малой системой.
Характер связи с внешней средой. По этому признаку все множество систем делят на детерминированные и стохастические системы.
В детерминированной системе состояние выхода жестко функционально связано с состоянием входа. Рассмотрим систему с единственным входом и единственным выходом.
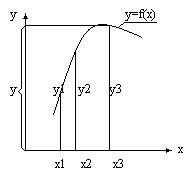
Для такой системы y = f(x), что позволяет представить ее поведение в декартовой системе координат. Зависимость выхода y от входа x представляет собой график, который называется переходной характеристикой. Детерминированная система отличается тем, что в ней связь выхода y и входа x имеет функциональный, жесткий характер: определенному значению x на входе соответствует вполне определенное значение y на выходе.
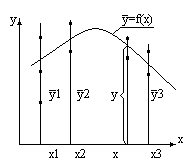
В стохастической системе ![]() не является в математическом смысле функцией. Наблюдается корреляция у от х, может быть составлено уравнение регрессии
не является в математическом смысле функцией. Наблюдается корреляция у от х, может быть составлено уравнение регрессии ![]() . Каждому значению входа x теперь соответствует значение y, находящееся в интервале значений. Связь имеет менее жесткий характер, и можно лишь утверждать, что при заданном x на входе y на выходе с определенной вероятностью примет значения из интервала. Причина здесь в том, что на систему оказывают влияния возмущения. Стохастические системы являются более общим случаем систем, лишь при определенных обстоятельствах мы можем пренебречь возмущениями и описывать систему как детерминированную.
. Каждому значению входа x теперь соответствует значение y, находящееся в интервале значений. Связь имеет менее жесткий характер, и можно лишь утверждать, что при заданном x на входе y на выходе с определенной вероятностью примет значения из интервала. Причина здесь в том, что на систему оказывают влияния возмущения. Стохастические системы являются более общим случаем систем, лишь при определенных обстоятельствах мы можем пренебречь возмущениями и описывать систему как детерминированную.
Зависимость характеристик систем от времени. По этому признаку системы делят на динамические и статические.
Статические системы отличаются тем, что их выход зависит только от состояния входов и не зависит от времени. Рассмотрим поведение простейшей статической системы, имеющей только один вход и выход во времени. Состояние входа системы х в некоторый момент времени, который мы примем за нуль, изменяется скачком, мгновенно от х1 до х2. Например, проводится очистка раствора от примесей. Проступающий на очистку раствор содержится в емкостях 1 и 2. В первой емкости содержание примеси в растворе составляет 5 г/л, а во второй 10 г/л. В некоторый момент времени раствор в первой емкости закончился и установка по очистке раствора переключается на вторую емкость. Момент переключения и будет нулевым моментом времени.
Установка позволяет выделить 90% примеси из раствора, следовательно, на ее выходе установится концентрация примеси, равная 0.1 от входной. До переключения емкостей выходная концентрация была равна 0.5 г/л, а после переключения она достигнет 1 г/л. Если инерция установки была бы равна нулю, выходная концентрация также мгновенно достигла бы нового значения. Это был бы пример статической системы, показанный ниже на рисунке.
![clip_image015[1] clip_image015[1]](/images/stories/clip_image0151_thumb_50eeb84a4fd7b29fd64a30b72b309394.gif)
y = f(x) – Выход такой системы не зависит от
времени, а зависит только от входа.
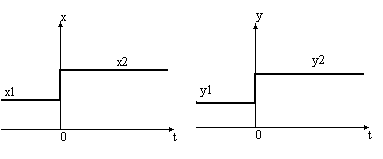
 а).
а).
Более общим свойством систем является то, что они проявляют динамические свойства. В некоторых случаях динамическими свойствами системы можно пренебречь и рассматривать её, как статическую.
Инерция технологических систем в металлургии цветных металлов довольно существенна (например, расплав в плавильной печи находится в течение многих часов), и в ряде случаев при моделировнии системы ей пренебречь нельзя.
Если переходный период короткий, изменения на входе системы происходят относительно редко по сравнению с временем переходного периода, то такую систему можно рассматривать, как статическую.
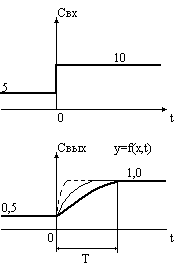 Состояние выхода системы зависит от состояния входа и выбора момента времени.
Состояние выхода системы зависит от состояния входа и выбора момента времени.
Как видно на рисунке, в динамической системе изменения на выходе не происходят мгновенно вслед за изменениями на ее входе. После истечения достаточно большого времени достигается новое значение выходной величины, и если на входе поддерживается постоянное значение, то состояние выхода далее также не изменяется. Такое состояние выхода называется новым установившимся значением.
Т – время переходного процесса, зависит от инерции.
Однако в течение некоторого времени состояние выхода изменяется от некоторого существовавшего ранее до нового установившегося значения, хотя состояние входа достигло нового значения и далее остается неизменным. На протяжении этого отрезка времени, которое называется переходным периодом, состояние выхода системы зависит также от момента времени.
Причиной этого является инерция системы. В нашем примере это объясняется тем, что установка для очистки раствора имеет некоторый собственный объем, заполненный раствором. В течение переходного периода не выходе установки мы будем наблюдать изменение концентрации примеси вследствие смешивания «старого» и «нового» очищенного раствора. Когда «старый» очищенный раствор будет практически вытеснен «новым», изменение концентрации примеси на выходе прекратится и будет достигнуто новое установившееся значение.
По типу входных и выходных величин системы делят на несколько классов.
а) непрерывные;
б) дискретные;
в)дискретно – непрерывные (системы массового обслуживания).
а) В системах непрерывного типа входные и выходные характеристики отображаются числами непрерывного ряда. Большинство технологических систем следует рассматривать, как системы непрерывные (составы, производительность, температура и другие параметры измеряются числами непрерывного ряда).
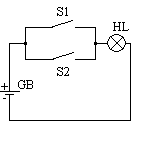
б) В дискретных системах состояние входных и выходных характеристик отображается дискретными величинами. Примером такой системы является показанная ниже на рисунке электрическая цепь, состоящая из источника тока, двух выключателей и лампочки. Выключатель является узлом с двумя возможными дискретными состояниями: он либо замкнут, либо разомкнут. Такие состояния можно отобразить дискретными числами, например 1 соответствует замкнутому, а 0 – разомкнутому состоянию выключателя. Выключатели являются также входами системы и определяют состояние лампочки, т.е. выхода системы. Лампочка также может находиться в одном из дискретных состояний: она либо горит (чему соответствует дискретное число 1), либо не горит (чему соответствует 0).
Модель такой системы представлена в таблице, где перечислены все ее возможные состояния. Кроме таблицы для описания подобных систем применяются известные в математике выражения алгебры логики (Булева алгебра).
В металлургии имеются системы, для описания которых иногда требуется применить такой подход.
|
Входы |
Выход |
|
|
S1 |
S2 |
HL |
|
0 1 0 1 |
0 0 1 1 |
0 1 1 1 |
Таким образом, входные и выходные характеристики изображаются дискретными числами, и состояние выхода зависит от входа.
в) В дискретно – непрерывных системах часть входных или выходных величин отображается числами непрерывными, другая часть – дискретными. В таких системах непрерывной величиной отображается время, а дискретными числами, как правило, отображается состояние элементов системы. Такие системы также называют системами массового обслуживания. Примером такой системы является расчетный узел любого магазина. Если представить его работу во времени, то нетрудно увидеть, что кассир имеет дело с потоком покупателей, причем момент, когда очередной покупатель подойдет к кассе, отображается непрерывным рядом чисел, т.е. время в такой системе непрерывно. Состояние кассира можно отобразить дискретными числами: он либо занят расчетом с покупателем (1), либо свободен и находится в состоянии ожидания очередного покупателя (0). Состояние 1 длится некоторое время, зависящее от ряда случайных факторов, например числа и особенностей покупок. Это время расчета с покупателем тоже измеряется непрерывным рядом чисел.
Задача моделирования подобных систем состоит в определении их пропускной способности, которая фактически является производительностью системы.
В металлургии достаточно примеров таких дискретно-непрерывных систем. Например, работу конвертерного отделения для переработки штейна можно рассматривать с позиций теории систем массового обслуживания. При этом надо учесть, что конвертер является устройством с двумя возможными состояниями: он либо находится под дутьем, т.е. совершает полезную работу по переработке штейна, либо находится в состоянии вспомогательных операций (ожидание заливки штейна, заливка штейна, слив шлака), когда дутье не подается и полезная работа не совершается. Конечно, производительность конвертерного отделения зависит от того, какую часть времени составляют полезная работа и ожидание, и в данном случае цель моделирования состоит в определении вероятности пребывания конвертера в состоянии полезной работы.
Другим примером таких систем является работа электролизных ванн в цехе электролиза, работа мостовых кранов в пролете металлургического цеха и т.п.

По уровню организации системы и задачам различают системы, показанные ниже на рисунке.

АСНИ – Автоматизированные системы научных исследований.
АСУТП – Автоматизированные систему управления технологическими процессами.
САПР – Системы автоматизированного проектирования.
ОАСУ – Организационные автоматизированные системы управления.
Функции АСНИ – исследование технологических систем на уровне отдельно взятых физико-химических явлений, технологических процессов или целых технологий. Оптимизация предполагает поиск наилучших условий работы технологической системы.
Прямое технологическое управление – функция АСУТП, – означает предварительный поиск оптимальных условий и поддержание этих условий по ходу технологического процесса. Сами оптимальные условия не постоянны во времени, они зависят, в частности, от состава перерабатываемого сырья.
САПР предназначены для создания новых технологий. В процессе их работы просчитываются многочисленные варианты технологии, отличающиеся, например, составом исходного сырья, набором технологических операций, применяемых для их осуществления аппаратов. По результатам этих многовариантных расчётов, на основе заранее определённых критериев оптимальности выбирается наилучший вариант.
ОАСУ существуют на многих предприятиях, как правило, решают задачи текущего управления в целом, анализы его работы и планирование работы предприятия в будущем. В составе систем есть подсистемы учёта, анализа, планирования материально-технических ресурсов, учёта труда и заработной платы, бухгалтерского учёта, оборота финансовых средств и т.д.
Метод построения модели выбирается с учётом свойств системы.
Моделирование технологических процессов и объектов
Основные понятия и определения
Модель – есть отражение наиболее существенных сторон моделируемого объекта.
Моделируемый объект – технологическая система.
Субъект моделирования – специалист предметной области (в нашем случае – инженер-металлург), создающий модель. Таким образом, всякая модель содержит субъективный фактор. Основная роль субъекта моделирования состоит в определении существенных свойств объекта, которые должны быть включены в модель. Существенные признаки объекта выбираются, исходя из цели создания модели и из особенности моделируемого объекта.
Модель и моделируемый объект не являются идентичными: модель является аналогом объекта моделирования.
Для объекта моделирования в металлургии наиболее существенными являются физико-химические процессы, являющиеся основой той или иной технологии. Таком образом, модели металлургических процессов и объектов в первую очередь должны включать описания химических взаимодействий, сопровождающие эти взаимодействия явления тепло- и массопереноса, гидродинамические особенности работы, теплообменные процессы и т.д.
Различают два существенно отличающихся между собой класса моделей:
1. модели – объекты;
2. концептуальные модели.
Отличительной особенностью моделей-объектов первого типа является то, что они воспроизводят однородный физический процесс, происходящий в моделируемом объекте. Например, для изучения движения газов и запыленности газового потока в печи создают физическую модель, которая является уменьшенной масштабной копией печи. Через такую модель пропускают поток газа (или жидкости), воспроизводя однородный с моделируемым объектом процесс движения газа. Для того, чтобы увидеть картину течения, газ в модели смешивают с дымом. Такие модели создаются на основе использования методов физического моделирования.
В отличие от моделей объектов, концептуальные модели не являются геометрическим подобием объектов, они не воспроизводят физический процесс, а представляют собой совокупность процедур, правил, связей, закономерностей, применяя которые, мы можем достоверно описать моделируемый объект. Для записи этих процедур и правил могут использоваться различные средства:
· естественный язык – семантическая модель (например, технологическая инструкция). Описания с помощью естественного языка часто неоднозначны и не позволяют описать объект количественно.
· если в качестве средства описания использованы средства математики, то мы имеем дело с математической моделью. Математически средства описания объектов моделирования могут быть различными:
а)могут использоваться аналитические средства: модель является уравнением или совокупностью уравнений различного вида;
б)алгоритм;
в)график;
г)таблица.
Независимо от класса, к которому принадлежит модель, она должна удовлетворять двум основным требованиям к моделям:
1. Экономичность. Это требование означает, что исследования, которые могут быть выполнены с помощью модели, должны обеспечить экономию времени и материальных средств по сравнению с экспериментом на объекте. Здесь нужно иметь в виду, что некоторые исследования принципиально не могут быть проведены непосредственно на объекте моделирования.
2. Традуктивность – возможность переноса результатов моделирования с модели на моделируемый объект. Пусть, например, задача моделирования состоит в изучении особенностей течения газов в рабочем пространстве печи и нас интересует, при каких условиях (т.е. при какой скорости течения) характер течения газа в печи станет турбулентным. Для ответа на этот вопрос проведем исследования на физической модели, являющейся геометрически уменьшенной масштабной копией печи. Пусть размеры печи соответствуют lо, а соответствующие им размеры модели lм. Характер течения газа зависит от величины критерия Рейнольдса:
![]() , где ν – вязкость, w – скорость, l – размер.
, где ν – вязкость, w – скорость, l – размер.
В теории подобия, являющейся теоретической основой методов физического моделирования, утверждается, что подобие модели и моделируемого объекта достигается тогда, когда одинаковы величины основных критериев подобия в модели и моделируемом объекте.
Reм = Reо
Выразив величины критериев Рейнольдса в модели и моделируемом объекте, получаем выражение, которое позволит нам определить, при какой скорости газа в печи характер течения будет турбулентным, если известна (измерена нами экспериментально) такая скорость в модели и известен геометрический масштаб уменьшения модели.
![]() =>
=> ![]() .
.
Как видим, недостаточно измерить скорость турбулизации потока в модели, необходимо еще знать, как пересчитать результат измерения на модели и применить его на моделируемый объект. Это и есть правило традукции, и в случае физической модели оно устанавливается на основе теории подобия.
Для математических моделей правило традукции базируется на аналогии дифференциальных уравнений, описывающих сходные свойства объекта и модели. Правила традукции выводятся на основе применения фундаментальных физических и химических законов.
Существует принципиально два пути построения модели объекта, если речь идет о математической модели:
· эмпирический;
· структурный.
Эмпирический подход применяется широко. Для построения модели в этом случае не требуется знать внутреннюю структуру моделируемого объекта, т.е. его элементы, характер связей между ними, нет необходимости знать, как описать эти связи количественно.
Эмпирический подход носит также название метода «черного ящика», поскольку наши знания о моделируемом объекте не позволяют определить его внутреннюю структуру. Применительно к металлургическому процессу или объекту это означает, например, что нам неизвестны основные физико-химические взаимодействия, мы не знаем, какие именно химические реакции происходят в объекте и в какой последовательности они осуществляются, как полно завершаются и с какой скоростью протекают. Остается представить объект как систему с ее входами и выходом в виде «черного ящика», внутреннее устройство которого и функционирование нам неизвестно. Но для практических целей было бы достаточно ответить на вопрос, каково будет состояние такой системы при известных величинах на ее входах. Для ответа не вопрос достаточно закономерным образом изменять состояния входов системы и наблюдать при этом, как изменяется состояние ее выхода в ответ на изменение состояния входов. В простейшем случае можно зафиксировать состояния всех входов, кроме одного. Изменяя величину на этом входе (температуру, например), получим зависимость выходной величины (например, извлечения металла в раствор при выщелачивании) от этого фактора.
Эта зависимость в общем случае может быть нелинейной, а ее график будет представлен некой кривой. Из математики известно, что нелинейные функции могут быть представлены с помощью их разложения в ряд. Используя такой подход можно любую функцию представить в виде полинома n-ной степени. Основная задача в процессе построения такой модели сводится к определению коэффициентов полинома b0,b1…..bn. Приемы построения таких моделей широко известны и приводятся в многочисленных литературных источниках. Более того, алгоритмы создания таких моделей реализованы в статистических пакетах прикладных программ, доступных для использования практически на любом персональном компьютере. От инженера-металлурга, желающего на основе использования эмпирического подхода получить модель технологического процесса, требуется только корректно провести системный анализ и выделить входы и выход системы.
у = b0 + b1x + b2x2 + … + bnxn – если влияет 1 вход.
К сожалению, эмпирические модели имеют существенный недостаток. Коэффициенты, входящие в полином, не обладают каким-либо физико-химическим смыслом. Их величина и знак в лучшем случае позволяют судить о направлении и силе влияния того или иного входа на выход, но не дают информацию о причинах этого влияния. Это ограничивает применение эмпирических моделей. К тому же эмпирические модели обладают нулевой прогностической мощностью: они могут быть использованы только тогда, когда изменение x на входе системы находится в пределах исследованного диапазона.
При использовании структурного подхода необходимо знать внутреннюю структуру, её элементы и связи. Модель объекта создается на основе описания всех элементов и связей. Такое описание использует фундаментальные законы: закон сохранения вещества, закон сохранения энергии, закон эквивалентов, термодинамические законы и др. Для каждого элемента системы записываются материальный и тепловой балансы, которые затем объединяются в общее описание моделируемого объекта.
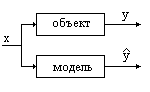
Независимо от того, на основе какого подхода создана модель, необходима оценка ее качества. На этом этапе необходим эксперимент с участием объекта моделирования. Идея состоит в том, что одинаковые значения входных величин задаются на соответствующих входах объекта и модели, как показано на рисунке. Состояние выхода объекта у измеряется экспериментально, величина на выходе модели равна y^. Используя полученную модель, проводят расчет выхода и получают предсказанное значение y^. Для каждого состояния входа и выхода можно вычислить отклонение у-у^. Если повторить эксперимент многократно, изменяя состояния входа и фиксируя состояния выхода, возвести в квадрат и просуммировать все квадраты отклонений, получим их сумму.
Критерием качества модели может быть (и чаще всего является) минимум суммы квадратов отклонения выходной величины, наблюдаемой на объекте и выходной величины, предсказанной с помощью модели. Чем меньше сумма квадратов отклонений, тем лучше модель воспроизводит моделируемый объект.
![]() → min – сумма квадратов отклонений должна
→ min – сумма квадратов отклонений должна
быть минимальной.
Алгоритм создания модели
Выбор метода создания модели зависит от свойств моделируемого объекта. В целом алгоритм создания модели иллюстрирует следующий рисунок.
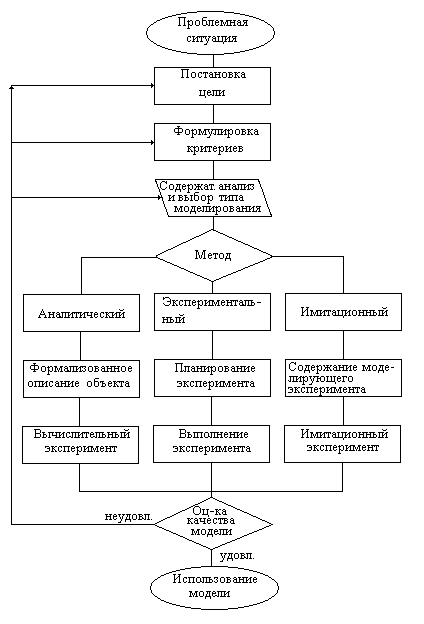
Проблемная ситуация возникает, как правило, когда изменяется внешние условия функционирования технологического объекта. Это означает изменение либо на входе, либо на выходе (например, изменение состава перерабатываемого сырья, повышение требований к качеству готовой продукции). Изменившиеся условия требуют адекватных изменений в технологическом объекте. Необходимо ответить на вопрос о том какие изменения в работе технологического объекта необходимы для достижения поставленной технологической цели при изменившихся условиях.
Постановка цели – определение цели создания модели.
Цели создания модели могут быть различными:
· уточнение закономерностей, управляющих технологическим процессом;
· модель создаётся, как инструмент для прогнозирования поведения объекта;
· для поиска оптимальных условий работы технологических объектов.
· для прямого оптимального управления технологическим процессом (в результате поиска оптимальных условий найденные оптимальные условия используются для управления технологическим процессом).
Формулировка критериев. Необходимо оценить критерии для оценки качества модели.
Содержательный анализ и выбор типа модели. Применяя методы системного подхода необходимо определить границы моделируемой системы, выделить ее из внешней среды и определить ее входы и выходы. На следующем этапе системного анализа выявляется внутренняя структура объекта, определяются его элементы и связи этих элементов, образующие структуру моделируемого объекта. На этом этапе становится понятно, к какому классу в соответствии со своими свойствами принадлежит моделируемый объект. Завершение содержательного анализа является выбор метода построения модели. Здесь возможны три дальнейших направления.
Аналитический метод или структурный подход. Используется для детерминированных систем с известной нам структурой внутренних связей.
Экспериментальный метод или эмпирический подход применяется для стохастических систем, подверженных действию возмущений, которыми нельзя пренебречь. Характер и величина возмущений при этом нам неизвестны, и учесть их действие аналитическим методом невозможно. Экспериментальный подход также является единственным выбором для систем, внутренняя структура которых нам недостаточно известна.
Имитационный метод используется для некоторых классов систем, например дискретно-непрерывных систем массового обслуживания.
После выбора метода построения модели содержание дальнейших шагов определяется выбранным методом.
Составление формализованного описания. На этом этапе, используя установленную структуру связей объекта и, применяя фундаментальные законы, создают математическое описание моделируемого объекта. Таким образом, модель в этом случае представляет собой алгоритм вычислений, уравнение или систему уравнений различного вида. Выполняя расчёты по этому алгоритму, решая системы уравнений, по заданным начальным условиям, можно рассчитать состояние выхода объекта. Наиболее популярными формами описания для металлургических процессов и объектов является материальный и тепловой баланс. Уравнения материального и теплового балансов могут быть записаны в дифференциальной или интегральной форме.
Планирование эксперимента. На этом этапе выбирается количество опытов, условия каждого опыта, т.е. сочетание факторов на входе системы в каждом проводимом опыте.
Выполнение эксперимента – выполнение запланированных опытов. В частности, для системы с тремя входами х1,х2,х3 и выходом у при постановке полного факторного эксперимента потребуется провести количество опытов 23=8. В этих опытах сочетания величин факторов на входе не повторяются. Величины на входах будем задавать на двух уровнях, т.н. верхнем и нижнем, изменяя их в пределах выбранного диапазона. Например, температура в технологическом объекте может быть в пределах 1100-1300 оС. Для оценки влияния температуры на процесс будем проводить опыты либо при нижнем, либо при верхнем значении температуры из этого диапазона. Обозначим верхний уровень знаком плюс, а нижний уровень знаком минус. Тогда матрица планирования эксперимента будет соответствовать ниже приведенной таблице. Для ее построения выделим три столбца, соответствующие факторам на входе и столбец для выходной величины, которую обычно именуют откликом. В столбцах факторов будем чередовать значения на верхнем и нижнем уровнях, причем в каждом правом столбце будем чередовать значения вдвое реже по сравнению с левым. В результате получаем матрицу эксперимента с неповторяющимися значениями факторов.
Для исключения влияния возмущений и случайных ошибок (связанных, например, с погрешностями измерения отклика) опыты проводят в случайной последовательности, например, первым проводят опыт, условия которого соответствуют третьей строке матрицы, вторым по порядку проводят опыт с условиями, соответствующими восьмой строке и т.д. Каждый раз измеряют значение выходной величины (отклика) и записывают результат в соответствующую строку матрицы, как показано в таблице.
Обработка результатов опыта подробно изложена в литературе и проводится в соответствии с известным алгоритмом. В результате такой обработки модель является полиномом первого порядка, содержащим свободный член и слагаемые, в которых присутствует коэффициент и значение фактора в первой степени.
Очень важно, что при таком планировании эксперимента матрица планирования обладает свойством ортогональности, а это позволяет выделить влияние каждого фактора на отклик отдельно от остальных факторов. Таким образом, величины коэффициентов в уравнении показывают направление и силу влияния каждого фактора на отклик. Если коэффициент при данном факторе имеет положительный знак и большую величину, то увеличение этого фактор а способствует увеличению отклика. Как в любой эмпирической модели, величины коэффициентов b0, b1, b2, b3 показывают степень проявления данных факторов, но они не имеют явного физико-химического смысла, т.е. не объясняют, почему какие-то факторы оказывают большее действие на отклик по сравнению с другими.
|
х1 |
х2 |
х3 |
|
|
+ |
+ |
+ |
у4 |
|
- |
+ |
+ |
у5 |
|
+ |
- |
+ |
у1 |
|
- |
- |
+ |
у8 |
|
+ |
+ |
- |
у3 |
|
- |
+ |
- |
у7 |
|
+ |
- |
- |
у6 |
|
- |
- |
- |
у2 |
![clip_image034[1] clip_image034[1]](/images/stories/clip_image0341_thumb_9b08685fcef6f10751896fecdfbe99ae.gif)
у = b0 + b1x1+ b2x2 + b3x3
Имитационное моделирование применяется для создания моделей дискретных или дискретно-непрерывных систем. Такие системы плохо описываются аналитически и затруднительно изучаются экспериментально. Модель создаётся как моделирующий алгоритм, воспроизводящий работу моделируемого объекта.
Структурный подход для построения математических моделей
При использовании структурного подхода, технологические объекты могут быть описаны на одном из следующих пяти уровней:
1.Молекулярный.
Металлургические процессы и объекты на этом уровне описываются как совокупность физико-химических явлений, в частности как совокупность химических реакций.
Например, конвертирование медного штейна в первом периоде на молекулярном уровне может быть описано основной химической реакцией окисления сульфида железа, входящего в состав штейна:
FeSж + O2г↑ + SiO2тв → 2FeO·SiO2ж + SO2г↑.
Исходными веществами-участниками этой реакции являются сульфид железа, кислород подаваемого дутья и кремнезем флюса. Продуктами реакции выступают фаялит (основной компонент шлака) и диоксид серы, удаляющийся в газовую фазу.
На молекулярном уровне описание объекта сводится к описанию стехиометрических соотношений масс исходных веществ и продуктов, равновесия и кинетики основных химических реакций.
2.Уровень малого объёма.
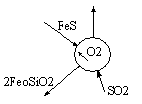 Пузырёк, капля, твердая частица – элементы малого объёма.
Пузырёк, капля, твердая частица – элементы малого объёма.
При описании конвертирования на уровне малого объема следует учесть дополнительно, что реакция первого периода конвертирования является гетерогенной, происходит на поверхности элемента малого объема, каковым в данном случае является пузырек газа, всплывающий в расплаве. Первоначально пузырек образуется при распаде струи подаваемого в расплав дутья и содержит внутри кислород и азот. Окисление сульфида железа происходит на его поверхности и сопровождается переносом вещества из объема расплава и газового пузырька к этой поверхности. Образующийся диоксид серы отводится внутрь пузырька, а 2FeOSiO2- в объем расплава. Это показано на рисунке. Для осуществления этой реакции отведено ограниченное время, поскольку пузырек всплывает в объеме расплава. Это время определяется скоростью движения пузырька и толщиной слоя расплава.
3.Уровень рабочей зоны аппарата. В дополнение к описанию предыдущего уровня необходимо учесть, что пузырек в расплаве не один. Одновременно в рабочей зоне присутствуют элементы малого объема в большом количестве. Рабочая зона характеризуется суммарной площадью поверхностей малых объёмов. К тому же, пузырьки имеют разные размеры, и необходимо учесть распределение размеров пузырьков и их средний размер суммарную поверхность.
4.Уровень технологического аппарата в целом. На этом уровне следует учесть, что помимо рабочей зоны аппарат имеет также и другие части, например устройства загрузки сырья и отвода продуктов, функционирование которых существенным образом сказывается на результатах работы всего моделируемого объекта. Так, скорость загрузки компонентов сырья или подачи дутья может лимитировать производительность технологического аппарата, хотя собственно физико-химические превращения осуществляются достаточно быстро.
5.Уровень технологической схемы. Моделируемый объект описывается на этом уровне как совокупность технологических операций, осуществляющихся последовательно. В технологических схемах существует большое количество оборотов, когда полученные полупродукты возвращаются на предыдущие технологические операции. На уровне технологической схемы каждая операция или технологический аппарат является объектом с сосредоточенными параметрами.
Использование структурного подхода для составления моделей на молекулярном уровне
Описание технологического процесса или объекта на молекулярном уровне означает описание следующих его сторон:
1.Описание стехиометрических соотношений между компонентами сырья, получаемых продуктов и вспомогательных материалов в системе химических реакций, составляющих сущность данного процесса.
2.Описание равновесия в системе обратимых химических реакций, которыми сопровождается процесс.
3. Описание скорости (кинетики) химических реакций.
Описание стехиометрии системы химических реакций
Реальные технологические процессы редко отображаются одной химической реакцией. Обычно процесс является совокупностью химических реакций, идущих одновременно во времени и пространстве. Часть химических реакций можно рассматривать как основные, другая рассматривается как побочные. При описании отдельной химической реакции используется закон эквивалентов, и никаких трудностей при этом не возникает. Например, горение углерода до диоксида описывается простой химической реакцией:
С + О2 = СО2
1м 1м 1м
12г 32г 44г.
Сложность описания возникает в том случае, когда несколько химических реакций осуществляются в едином реакционном пространстве в одно и то же время, а как раз это и происходит в любом технологическом процессе. При этом возможно осуществление последовательных, параллельных, обратимых химических реакций и их сочетание. Для расчетов стехиометрических соотношений в таких системах существует несколько методов.
Метод направленных графов
Граф – это фигура, построенная из элементов двух типов: вершин, которые изображаются в виде окружностей и связей, представляющих собой линии, направленные от вершины к вершине. Связи графа характеризуются направлением.
Вершины графа отображают массы веществ, а связи – переход веществ из одних в другие в ходе химической реакции. Применение метода направленных графов рассмотрим на следующем примере. Пусть технологический процесс является совокупностью следующих химических реакций:
![]()
A + 2B → 2C (1)
A → 2D (2)
C → E + H (3)
D → 2F + H (4).
Вещества А и В являются исходными, С и D – промежуточными, а Е, H и F – конечными продуктами реагирования. Как видно на схеме, процесс содержит последовательные и параллельные химические реакции. В частности С вначале образуется по реакции (1), а затем расходуется по реакции (3), аналогично D образуется по реакции (2) и расходуется по реакции (4). Компонент А параллельно расходуется по реакциям (1) и (2). Очевидно, что в этом случае ответить на вопрос о том, какая масса вещества участвует в каждой из реакций более сложно, чем для отдельно протекающей химической реакции.
Для ответа на этот вопрос построим направленный граф, который позволяет изобразить путь всех химических реакций и массы всех участвующих в них веществ.
Пусть для упрощения дальнейших рассуждений в системе в начальный момент времени отсутствовали промежуточные вещества C и D, а также конечные продукты реагирования E, F и H.
Построение графа начнем с начальных веществ. Вершиной 1 обозначим исходную массу А в системе. Часть вещества А расходуется по реакциям (1) и (2), обозначим ее вершиной 2. Другая часть А останется в системе, и эту остаточную массу А обозначим вершиной 3. Как видно на схеме, израсходованная масса А связана с реакциями (1) и (2), обозначим соответственно вершиной 4 расход вещества А по реакции (1), а вершиной 5 – расход вещества А по реакции (2).
Такие же рассуждения проведем в отношении вещества В. Исходную массу В в системе обозначим вершиной 6, расход В в реакции (1) изобразим вершиной 7, а остаток В в системе – вершиной 8.
Обратим внимание на реакцию (1). Продуктом ее является промежуточное вещество С, которого в начальный момент в системе не было. Обозначим массу С, образующуюся по реакции (1) вершиной 9. В реакции (1) принимают участие вещества А в количестве, соответствующем вершине 4, и В, в количестве, соответствующем вершине 7. Следовательно, необходимо направить связи от вершин 4 и 7 к вершине 9. Часть вещества С, являющегося промежуточным, расходуется по реакции (3). Отобразим эту массу С вершиной 11, другая часть С остается в системе, что отображает вершина 10.
Расход С обусловлен его участием в реакции (3), продуктами которой являются вещества Е и Н. Обозначим массу вещества Е, образующуюся по реакции (3) вершиной 12, а массу вещества Н, образующуюся по этой же реакции вершиной 13. Заметим, что Н образуется также и в ходе реакции (4).
Другое направление процесса связано с реализацией реакции (2), в которой принимает участие вещество А в количестве, соответствующем вершине 5. Продуктом реакции 2 является вещество D, массу которого отобразим вершиной 14.
Часть промежуточного вещества D далее разрушается в ходе реакции (4), эту массу D обозначим вершиной 15, а другая часть останется в системе, что соответствует вершине 16.
Реакция (4) идет сообразованием веществ F и Н. Масса образующихся в ней веществ обусловлена расходом D в количестве, соответствующем вершине 15. Обозначим вершиной 18 массу вещества F, образующуюся по реакции (4), а вершиной 17 – массу вещества Н, образующуюся по этой же реакции. Общую массу вещества Н в системе обозначим вершиной 19. Полученный граф, приведенный ниже на рисунке, полностью отображает ход всех химических реакций в рассматриваемой системе.
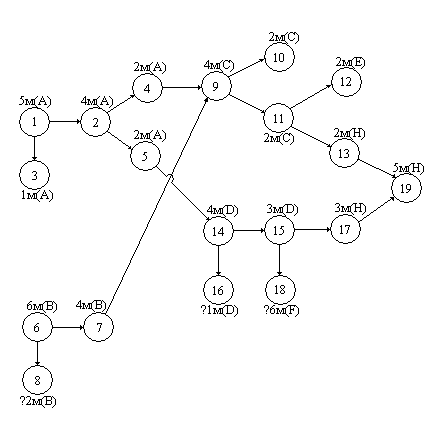
1 – начальная масса вещества А в системе.
2 – расход вещества А по реакциям (1) и(2).
3 – остаток вещества А в системе.
4 – масса вещества А, участвующего в реакции (1).
5 – масса вещества А, участвующего в реакции (2).
6 – начальная масса вещества В в системе.
7 – расход вещества В по реакции (1).
8 – остаток вещества В в системе.
9 – масса вещества С, образующегося по реакции (1).
10 – остаток вещества С в системе.
11 – расход вещества С по реакции (3).
12 – масса вещества Е, образующегося по реакции (3).
13 – масса вещества Н, образующегося по реакции (3).
14 – масса вещества D, образующегося по реакции (2).
15 – масса вещества D, израсходованного в реакции (4).
16 – остаток вещества D в системе.
17 – количество вещества F, полученного по реакции (4).
18 – количество вещества Н, полученного по реакции (4).
19 – общая масса вещества Н в системе.
Пусть все реакции осуществляются в изолированной по веществу системе, а компоненты находятся в растворе. В начальный момент времени концентрации исходных веществ равны: СА0 = 5моль/дм3; СВ0 = 6моль/дм3. В системе отсутствуют промежуточные и конечные продукты: СС0 = СD0 = СE0 = СF0 = СH0 = 0 моль/дм3.
Спустя некоторое время отобрали пробу раствора и определили текущие концентрации веществ: СА = 1моль/дм3; СН = 5моль/дм3; СС = СЕ =2моль/дм3. Остальные концентрации определить не удалось. Как рассчитать СВ, СF, СD?
Если дальнейшие рассуждения провести для объема системы, равного 1 дм3, то значения концентраций веществ численно совпадут с их массами.
Далее начнем движение по графу от известных вершин. В частности, начальная масса А равна 5 моль, а текущая (остаточная) – 1 моль. Следовательно, расход А составил 4 моль. В отношении В мы не можем провести подобные вычисления, поскольку остаток В нам неизвестен. К тому же неясно, какая масса А расходуется по реакции (1), а какая по реакции (2).
Воспользуемся другим направлением, и будем двигаться по графу от продуктов к исходным веществам. В частности, вещество Е, образующееся по реакции (3) представляет конечный продукт, и его масса соответствует вершине 12. В этой же реакции принимают участие вещества С и Н, следовательно расход С по реакции (3) в вершине 11 равен 2 моль, и такая же масса Н образуется в вершине 13.
Общая масса образовавшегося Н равна 5 моль, из них 2 – по реакции (3), другие 5-3=2 моль образуются по реакции (4), что отображено вершиной 17. Отсюда следует, что в реакции (4) образуется удвоенное количество молей F, покажем его в вершине 18. Масса F в вершине 18 равна 6 моль. Расход D по реакции (4) равен числу молей Н, образующихся по этой реакции, что соответствует вершине 15.
Остаток вещества С в системе равен 2 моль, что показано в вершине 10, а его расход в вершине 11 также равен 2 моль. Следовательно, по реакции (1) образуется 4 моль вещества С (вершина 9), а это требует удвоенного расхода вещества В и такого же количества А (вершины 7 и 4 соответственно). Отсюда остаток В в системе равен 2 моль.
Расход вещества А по реакции (2) составляет 2 моль, при этом образуется по реакции (4) вещество D в количестве 4 моль. Расход D равен 3 моль (вершина 15), остаток D в системе равен 1 моль.
Ответ: СВ = 2моль/дм3, СD = 1моль/дм3, СF = 6моль/дм3.
Преимущество метода направленных графов состоит в наглядности изображения хода процесса, но решение задачи требует сложных логических построений.
Матричный метод
Помимо метода направленных графов существуют и другие методы решения стехиометрических задач для сложных систем химических реакций. Матричный метод позволяет свести задачу к такой форме, которая в наибольшей степени пригодна для дальнейшего ее решения с использованием компьютерной техники.
Рассмотрим решение предыдущей задачи с использованием матричного метода. В системе из 4 химических реакций принимают участие 7 веществ. Уравнения химических реакций с участием этих веществ можно записать так, как если бы в них участвовали все вещества одновременно. Если в какой-то химической реакции вещество не принимает участия, формально это означает, что стехиометрический коэффициент при этом веществе равен нулю. Условимся также, что стехиометрические коэффициенты для исходных веществ будем принимать положительными, а для продуктов – отрицательными. Тогда первое из химических уравнений системы химических реакций, рассмотренных в предыдущем примере, может быть записано следующим образом:
A + 2B - 2C + 0D + 0E + 0F + 0H = 0.
Рассуждая аналогично для всех веществ и всех реакций составим систему линейных уравнений, описывающих соотношение масс всех участвующих в реакциях веществ. Размерность системы 4х7, где 4- число уравнений, 7- число веществ, участвующих в химических реакциях. Матрица коэффициентов этих уравнений приведена ниже, а вектор-столбец нулевой.
К полученной системе уравнений необходимо добавить еще несколько уравнений, имеющих не нулевую правую часть. Эти уравнения записываются исходя из начальных условий задачи.
При определённых условиях, когда известны значения исходных и текущих масс некоторых компонентов системы, можно получить единственное решение методами линейной алгебры.
Описание систем путём расчёта стехиометрии химических реакций с практической точки зрения позволяет рассчитать массы всех участвующих веществ. Таким образом, можно прогнозировать поведение системы, состав продуктов, количество израсходованных веществ.
Стехиометрические расчёты предполагают, что все химические реакции в данном технологическом процессе идут до конца вправо.
Моделирование равновесия в системах химических реакций
Значительная часть химических реакций, составляющих основное содержание технологических процессов в цветной металлургии, являются обратимыми. Рассмотрим пример обратимой химической реакции:
А + 2В ![]() 2С.
2С.
Равновесие в такой химической реакции достигается при определенных значениях активностей участвующих веществ. Если эти вещества находятся в растворе, а их концентрации невелики (разбавленные растворы), то с некоторым приближением вместо величин активностей можно использовать величины концентраций. Равновесие в химической реакции характеризуется величиной константы равновесия:
![]() .
.
Величина константы равновесия связана с изменением энергии Гиббса и может быть рассчитана по термодинамическим данным участвующих веществ:
![]()
где ΔGT- изменение энергии Гиббса для данной химической реакции, Т – температура, R- универсальная газовая постоянная.
Рассчитав величину константы равновесия для химической реакции, идущей при заданной температуре, можно определить соотношение концентраций исходных веществ и продуктов, которое установится при достижении равновесия.
Несколько более сложно определить равновесный состав системы, в которой одновременно происходит несколько обратимых химических реакций. Рассмотрим следующий пример. Пусть имеется система обратимых химических реакций с участием веществ А, В, С и D. В данной системе вещество А последовательно и обратимо превращается в вещество С, предварительно образуя В. Возможен и параллельный путь: вещество А параллельно с образованием В разлагается с образованием D. При заданных условиях (температуре, давлении) в системе установится равновесие и будут достигнуты равновесные концентрации веществ.
Для расчета равновесных концентраций запишем выражения для констант равновесия всех реакций через равновесные концентрации:
![]() А
А ![]() В
В ![]() ;
; ![]()
В ![]() С
С ![]() ;
; ![]()
А ![]() D
D ![]() ;
; ![]() .
.
Пусть в начальный момент отсутствуют промежуточные вещества В и С, а также конечный продукт D:
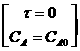 ; СВ0=0; СС0=0; CD0=0.
; СВ0=0; СС0=0; CD0=0.
Значения констант равновесия рассчитаем для каждой из реакций по термодинамическим данным: ![]() . Таким образом, величины констант равновесия будем считать известными величинами.
. Таким образом, величины констант равновесия будем считать известными величинами.
На единицу объёма данной системы СА0 – СА представляет собой количество израсходованных молей компонента А. В соответствии со стехиометрией химических реакций и законом сохранения вещества, убыль массы А равна сумме масс образующихся веществ B,C и D, что можно выразить уравнением:
СА0 – СА = CB + CC + CD.
Преобразуем уравнение к следующему виду:
CA0 = CA + CB + CC + CD,
И подставим в правую часть выражения для соответствующих концентраций веществ:
CA0 = CA + k1CA + k1k2CA + k3CA.
Сгруппируем однородные члены уравнения
CA0 = CA(1 + k1 + k1k2 + k3)
и получим выражение для равновесной концентрации СА
![]() .
.
Равновесные концентрации других веществ легко определить, поскольку значения всех констант равновесия нам известны из предыдущего расчета, а выражения содержат CA.
При расчётах равновесий в системах химических реакций необходимо знать kр каждой реакции, начальный состав системы – это даёт возможность рассчитать равновесный состав системы.
Реальные задачи расчёта равновесного состава систем намного сложнее: уравнения в этих задачах нелинейны; требуется учесть, что компоненты, входящие в реакцию находятся в разных фазах; вместо концентраций корректно использовать значения активностей компонентов. Практический смысл расчёта равновесий в таких сложных системах сводится к тому, что расчётный равновесный состав системы является тем физико-химическим пределом, до которого может дойти реальный процесс, если для его осуществления отведено неограниченное время.
Моделирование кинетики химических реакций
В физической химии скорость химической реакции определяется в соответствии с уравнением:
![]() ,
,
где dq – изменение массы реагирующего вещества, моль.
dt – приращение времени, с.
V – мера реакционного пространства.
Различают гомогенные химические реакции, в которых все участвующие вещества находятся в пределах одной фазы (газовой или жидкой). Для таких реакций мерой реакционного пространства является объем, а размерность скорости будет: ![]() .
.
Гетерогенные химические реакции происходят между веществами, находящимися в разных фазах (газ-твердое, газ-жидкость, жидкость-жидкость, твердое-жидкость). Собственно химическая реакция при этом реализуется на поверхности раздела фаз, которая и является мерой реакционного пространства.
Для гетерогенных реакций размерность скорости иная: ![]() .
.
Изменение массы реагирующих веществ имеет свой знак. Для исходных веществ масса по ходу реакции убывает, изменение массы имеет отрицательный знак, и величина скорости принимает отрицательное значение. Для продуктов химической реакции масса возрастает, изменение массы положительно, знак скорости принимают также положительным.
Рассмотрим простую химическую реакцию
А + 2В = 2С.
К простым реакциям относятся те, которые осуществляются в одну стадию и идут до конца, т.е. являются необратимыми.
Определим скорость такой химической реакции. Для этого прежде всего необходимо решить, по какому из веществ будет определена скорость реакции: ведь А и В – исходные вещества, и изменение их масс отрицательно, а С является конечным продуктом, и его масса возрастает со временем. Кроме того, не все стехиометрические коэффициенты в реакции равны единице, а это значит, что если расход А за какое-то время равен 1 молю, расход В за это же время будет 2 моля, и соответственно значения скорости, рассчитанные по изменению масс А и В будут отличаться вдвое.
Для простой химической реакции можно предложить единую меру скорости, которая определяется следующим образом:
![]() ,
,
где ri – скорость по i-му участнику реакции
Si – стехиометрический коэффициент i-го участника реакции.
Стехиометрические коэффициенты для исходных веществ принимаются положительными, для продуктов реакции они отрицательны.
Если реакции идут в изолированной системе, не обменивающейся веществом с внешней средой, то только химическая реакция приводит к изменению масс вещества в системе, и, следовательно, их концентраций. В такой системе единственной причиной изменения концентраций С является химическая реакция. Для этого частного случая
![]() ,
,
Скорость химической реакции зависит от концентраций участвующих веществ и от температуры.
![]()
где k – константа скорости химической реакции, СА,СВ – концентрации веществ, n1, n2 – порядки по соответствующим веществам. Это выражение известно в физической химии как закон действующих масс.
Чем выше значения концентраций, тем выше скорость химической реакции.
Порядок (n) определяется экспериментально и связан с механизмом химической реакции. Порядок может быть целым или дробным числом, существуют также реакции нулевого порядка по каким-то веществам. Если порядок по i-му веществу равен нулю, то скорость химической реакции не зависит от концентрации этого вещества.
Значение скорости химической реакции зависит от температуры. В соответствии с законом Аррениуса константа скорости изменяется при изменении температуры:
![]()
где А – предэкспоненциальный множитель;
Е – энергия активации;
R – универсальная газовая постоянная, константа;
Т – температура.
Как и величина порядка реакции, величины энергии активации и предэкспоненциального множителя определяются для конкретной реакции экспериментально.
Если химическая реакция осуществляется в гетерогенном процессе, то на её скорость оказывает влияние так же процесс подвода исходных веществ и отвода продуктов из зоны химической реакции. Таким образом, имеет место сложный процесс, в котором имеются диффузионные стадии (подвод, отвод) и кинетическая стадия – собственно химическая реакция. Скорость всего процесса в целом, наблюдаемого в эксперименте, определяется скоростью самой медленной стадии.
Таким образом, влияя на скорость диффузионной стадии процесса (перемешивание), влияем на скорость всего процесса в целом. Это влияние сказывается на величине предэкспоненциального множителя А.
Большинство химических реакций не являются простыми (т.е. идут не в одну стадию и не до конца) – сложные химические реакции:
а) A![]() B – обратимые;
B – обратимые;
б) А→В; В→С – последовательные;
в) А→В; А→С – параллельные.
Для сложной химической реакции нет единой меры скорости. В отличие от простой, здесь можно говорить о скорости образования и разрушения каждого химического вещества. Таким образом, если в системе происходят химические реакции и участвуют n веществ, для каждого из n веществ есть своё значение скорости.
Для любого из веществ скорость образования и разрушения является алгебраической суммой скоростей всех стадий с участием этого вещества.
Скорость сложной химической реакции
Моделирование кинетики системы сложных химических реакций рассмотрим на следующем примере. Пусть имеется технологический процесс, суть которого отображается следующими химическими реакциями:
![]() k1; 1 по В
k1; 1 по В
![]()
![]() A + 2B C
A + 2B C
k2; 0,7 по С
k3; 1 по А; 0,35 по Н
![]() A 2D
A 2D
k4; 1 по С; 1 по D
![]()
![]() C + D 3Е
C + D 3Е
k5; 2 по Е;
![]()
rA = –k1CB + k2CC0.7 – k3CACH0.35
rB = –2k1CB + 2k2CC0.7
rC = k1CB – k2CC0.7 – k4CCCD + k5CE2
rD = k3CACH0.35– k4CCCD + k5CE2
rE = k4CCCD – 3k5CE2
rH = 0
Кинетические константы (порядки по веществам и значения констант скорости для стадий) определены экспериментально. На схеме процесса над стрелками, соответствующими стадиям, показаны величины порядков по веществам. Не указанные порядки нулевые.
В процессе принимают участие 6 веществ: А и В являются исходными, С и D – промежуточными, Е – конечный продукт, Н – катализатор одной из стадий. Три химические реакции имеют пять стадий, три из которых являются прямыми, две – обратными.
Все реакции осуществляются гомогенно и проходят в замкнутой по веществу системе, что дает основания использовать для характеристики скорости выражения:
![]()
.
На основании изложенного выше запишем выражения для скоростей по каждому веществу-участнику. Всего получим 6 выражений по числу веществ. Для каждого из веществ скорость расходования или образования есть алгебраическая сумма скоростей всех стадий с участием данного вещества. Так, веществ А участвует в трех стадиях, в первой в качестве исходного вещества, во второй- как продукт, в третьей вновь как исходное вещество. Слагаемые скорости для первой и третьей стадий будут отрицательны, для второй стадии скорость имеет положительный знак. Значения скорости для каждой стадии по закону действующих масс являются произведением константы скорости соответствующей стадии и концентраций веществ в степенях, равных порядкам по веществам. С учетом этого выражения для скоростей по веществам будут следующими:
![]()
![]() = –k1CB + k2CC0.7 – k3CACH0.35
= –k1CB + k2CC0.7 – k3CACH0.35
![]() = –2k1CB + 2k2CC0.7
= –2k1CB + 2k2CC0.7
![]() = k1CB – k2CC0.7 – k4CCCD + k5CE2
= k1CB – k2CC0.7 – k4CCCD + k5CE2
![]() = k3CACH0.35– k4CCCD + k5CE2
= k3CACH0.35– k4CCCD + k5CE2
![]() = 3k4CCCD – 3k5CE2
= 3k4CCCD – 3k5CE2
![]() = 0.
= 0.
Последняя скорость по веществу Н, катализатору третьей стадии, равна нулю. Масса катализатора не изменяется по ходу реакции.
В левой части всех уравнений присутствует производная концентрации вещества по времени, следовательно, уравнения кинетики являются дифференциальными. Концентрации в правой части уравнений в произвольный момент времени должны одновременно удовлетворять всем уравнениям, а это означает, что совокупность уравнений кинетики в математическом смысле есть система уравнений.
Модель химической кинетики является системой дифференциальных уравнений, решением которой является набор функций Ci = fi(t):
![]()
СА=f1(t)
СB=f2(t)
СC=f3(t)
СD=f4(t)
СE=f5(t)
СH=f6(t).
Для того, чтобы установить конкретный вид функций, необходимо решить систему дифференциальных уравнений, т.е. проинтегрировать систему уравнений кинетики. Интегрирование уравнений кинетики рассмотрим ниже на более простом примере, а после этого вновь вернемся к задаче, рассмотренной выше.
Интегрирование уравнений кинетики
Пусть идет химическая реакция разложения вещества А, в результате которой образуется вещество В. Экспериментально установлено, что она имеет первый порядок по концентрации А, а значение константы скорости для условий ее осуществления равно k. Это отображено на схеме реакции ниже.
k; 1 по А
![]() A В.
A В.
Скорость реакции равна ra = –kCA, или
![]() .
.
Определим начальные условия для решения дифференциального уравнения кинетики. Будем считать, что в начальный момент реакции нам известна концентрация вещества А, обозначим ее как САо. Запишем начальные условия в виде ![]() . Проинтегрируем полученное уравнение, используя интегралы с подстановкой пределов. Пределы интегрирования определяются из начальных условий: когда время равно нулю, концентрация А равна начальной, в произвольный момент t концентрация равна СА:
. Проинтегрируем полученное уравнение, используя интегралы с подстановкой пределов. Пределы интегрирования определяются из начальных условий: когда время равно нулю, концентрация А равна начальной, в произвольный момент t концентрация равна СА:
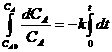 .
.
В результате интегрирования имеем:
![]() ,
,
заменяя разность логарифмов логарифмом частного имеем далее:
![]() ,
,
проводя потенцирование получим:
![]() .
.
После всех преобразований решение дифференциального уравнения представляет собой экспоненциальную убывающую функцию:
![]() .
.
Проверим, не противоречит ли полученное решение условиям нашей задачи. При t=0, т.е. в момент начала химической реакции СA=CA0, поскольку экспонента обращается в единицу. Действительно, в начальный момент концентрация вещества А равна начальной. При t→∞ экспонента с отрицательным показателем стремится по величине к нулю. За бесконечно большое время вследствие химической реакции все вещество разлагается и образует В.
Численные методы интегрирования
Вернемся теперь к предыдущей задаче. Очевидно, что интегрирование системы дифференциальных уравнений является более сложной задачей по сравнению с рассмотренной ранее. Применение аналитичееских приемов интегрирования вряд ли возможно, поскольку правые части дифференциальных уравнений содержат концентрации сразу нескольких веществ, и разделить переменные не удастся.
Воспользуемся численным методом интегрирования. Для этого разобьем ось времени на малые отрезки (шаги). Считая, что производные концентраций веществ по времени есть математический предел отношения приращений концентраций к приращению времени, при Δt ,стремящемся к нулю:
![]() ,
,
преобразуем систему дифференциальных уравнений в систему алгебраических. В левой части приращение времени нам известно, поскольку шаг по времени мы выбираем сами. Важно только то, что этот шаг должен быть малым.
В правой части значения всех констант скорости нам также известны из эксперимента, то же следует сказать и о величинах порядков. Подставим в правую часть также значения концентраций всех веществ, воспользовавшись начальными условиями. Каждое из уравнений системы содержит в этом случае лишь одну неизвестную величину – изменение концентрации ΔCi. По сути это изменение концентрации за первый шаг решения, когда время изменяется от нуля (начала химической реакции) до Δt. Изменение концентрации со своим знаком суммируем с начальной концентрацией и определяем концентрацию каждого из веществ на момент окончания первого шага решения.
На следующем шаге решения в правую часть подставим значения концентраций из предыдущего шага решения и вновь получим ΔCi, но теперь для следующего шага решения, как показано на рисунке.
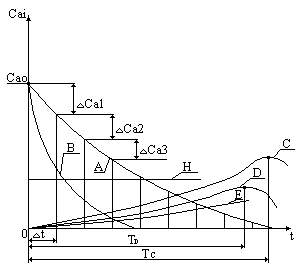
На каждом шаге решения получаем ординаты, соответствующие изменению концентрации всех веществ, участвующих в реакциях. Геометрическое место точек, являющихся ординатами, даст для каждого из веществ график функции изменения концентрации во времени. Заметим, что в результате численного интегрирования мы не получаем аналитического выражения, задающего изменение концентрации во времени, ординаты на графике получаются расчетным путем. Однако построение графиков функций изменения концентраций по времени возможно, а вид кривых позволяет сделать ряд выводов, имеющих практический смысл.
Очевидно, что концентрации исходных веществ со временем убывают, поскольку они расходуются в реакции. Не менее очевидно, что концентрации конечных продуктов возрастают.
Поведение промежуточных веществ заслуживает отдельного рассмотрения. Графики концентраций промежуточных веществ имеют максимумы, соответствующие определенной продолжительности реакции. Если промежуточное вещество является целевым продуктом химических реакций, то максимум концентрации соответствует оптимальной продолжительности для получения данного целевого вещества.
Так происходит потому, что в начальный момент химической реакции концентрации исходных веществ велики, а скорость химической реакции с участием исходных веществ пропорциональна их концентрациям. Реакции с участием исходных веществ вначале происходят с большими скоростями. Это означает, что промежуточные вещества образуются также с высокой скоростью.
С другой стороны, скорость разложения промежуточных веществ также пропорциональна их концентрации, и мала вначале. Скорость образования промежуточных веществ больше скорости их разложения, что способствует накоплению промежуточных веществ, их концентрация возрастает.
По мере развития химической реакции уменьшается скорость образования промежуточных веществ и растет скорость их разрушения. Когда величины скоростей становятся одинаковыми, рост концентрации прекращается, в системе наблюдается максимум концентрации промежуточного вещества.
Далее скорость образования промежуточного вещества снижается, поскольку продолжается уменьшение концентраций исходных веществ. Скорость разрушения промежуточного вещества также уменьшается, оставаясь по величине больше скорости образования, а это приводит к расходованию промежуточного вещества в системе и к падению его концентрации.
![]()
;![]()
ТС – оптимальное время для получения вещества С.
Рассмотрим поведение вещества С: в начальный момент времени СС = 0.
k1CB>k2CC0.7
Таким образом, моделирование кинетики позволяет определить образование и расходование всех веществ в системах химических реакций, установить вид функции концентрации в зависимости от времени, в ряде случаев определить оптимальные условия по ведению химической реакции.
Химические реакции в потоке вещества
Многие технологические аппараты работают в непрерывном режиме. Рассмотрим в качестве примера плавильную печь для переработки шихты из медных концентратов и флюсов. Схема такого аппарата приведена ниже на рисунке.
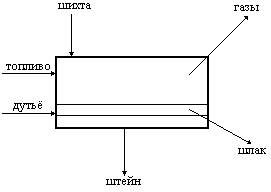 Непрерывный проточный аппарат представляет собой проточный реактор, в котором осуществляется определённый набор химических реакций.
Непрерывный проточный аппарат представляет собой проточный реактор, в котором осуществляется определённый набор химических реакций.
Наличие потоков вещества влияет на условия осуществления химических реакций.
Реальные потоки вещества обладают достаточно сложными свойствами:
· гидродинамический режим – ламинарный, турбулентный, переходный;
· число фаз – много- и однофазные.
Примером является поток, движущийся по трубе. Скорость движения потока в пределах одного сечения неодинакова: наибольшее значение скорости на оси потока, а вблизи стен за счет торможения потока силами вязкости эта скорость мало отличается от нуля. Однако, если объемный расход среды потока равен Q, а площадь сечения F, нетрудно определить среднюю скорость течения потока, равную Q/F.
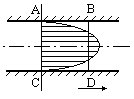 Q м3/c
Q м3/c
F м2
![]()
Еще больше сложностей возникает при описании многофазных потоков, а реальные потоки как раз чаще всего ими и являются.
В этой связи учитывать свойства реальных потоков при создании математической модели достаточно сложно. Поэтому для создания модели аппаратов проточного типа существует несколько идеализированных моделей течения потоков.
1. Модель идеального вытеснения – такая идеализированная модель потока основана на следующих допущениях (аппаратом такого типа может быть трубчатая обжиговая печь):
· поток стационарный, объемный расход среды не меняется во времени;

dV = F·dl
· в таком потоке скорости во всех точках потока одинаковы;
· элемент объёма dV в таком потоке является замкнутой по веществу системой (не обменивается с соседними элементами);
· в потоке идеального вытеснения отсутствует продольное перемешивание;
· поперечное перемешивание в потоке тоже отсутствует.
Другое название модели идеального вытеснения – поршневой поток.
Для моделирования кинетики в случае потока идеального вытеснения вполне годится подход, применимый к системам, изолированным по веществу.
Рассмотрим реакцию первого порядка, которая проходит в аппарате идеального вытеснения.
k1; 1 по А
![]() A В
A В
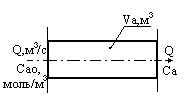 Создадим модель, позволяю-щую рассчитать выходную концен-трацию А. Константа известна, поря-док первый.
Создадим модель, позволяю-щую рассчитать выходную концен-трацию А. Константа известна, поря-док первый.

![]()
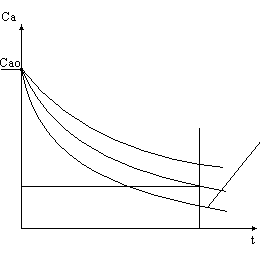
![clip_image112[1] clip_image112[1]](/images/stories/clip_image1121_thumb.gif)
![]()
![]() – время пребывания вещества в аппарате
– время пребывания вещества в аппарате
![]()
![]()
![]()
Чем больше константа скорости k, тем быстрее концентрация стремится к концентрации в точке выхода.
В пределах аппарата идеального вытеснения концентрация вещества не остаётся постоянной – она падает от концентрации в точке входа до концентрации в точке выхода.
2. Модель идеального перемешивания (аппаратом такого типа является, например, печь КС, гидрометаллургический реактор для выщелачивания и т.п.).
Допущения:
· поток стационарный, объёмный расход вещества (Q) через аппарат должен быть постоянным;
· концентрация во всех точках аппарата идеального перемешивания одинакова.

Следствием второго допущения является то, что концентрация вещества в точке выхода равна концентрации внутри аппарата.
![]()
Среднее время пребывания вещества в аппарате – ![]() .
.
Время пребывания различных порций потока в аппарате идеального перемешивания неодинаково.
Элемент объёма в таком аппарате является открытой системой, для такого аппарата не годится подход для замкнутой системы. Для описания кинетики в этом случае используем закон вещества и рассматриваем аппарат, как единое целое, концентрация во всех точках одинакова. На основании закона сохранения вещества запишем уравнение материального баланса для всего аппарата в целом (в единицу времени):
Приход – Расход = 0
Пусть в условиях аппарата идеального перемешивания происходит реакция разложения первого порядка:
k1; 1 по А
![]() A В
A В
Материальный баланс по веществу А будет суммой составляющих:
![]()
где:
1 слагаемое – число молей вещества А, вносимое потоком в единицу времени;
2 слагаемое– унос вещества из аппарата в единицу времени;
3 слагаемое– масса вещества, израсходованного в химической реакции. Разделим обе части уравнения на величину объемного расхода Q≠0:
![]()
![]() , откуда
, откуда
![]() .
.
Создадим для химических реакций одинаковые условия в том и другом аппарате (одинаковая температура, ![]() k1=k2). Допустим, что при определённой температуре k1=k2=1. зададим СА0 = 1 моль/м3. Vа = 1м3, Q1 = Q2 = 1м3/с. Тогда:
k1=k2). Допустим, что при определённой температуре k1=k2=1. зададим СА0 = 1 моль/м3. Vа = 1м3, Q1 = Q2 = 1м3/с. Тогда:
![]()
![]() .
.
Удивительно то, что результат одной и той же химической реакции оказывается в разных аппаратах разным. Более эффективным является аппарат идеального вытеснения, в котором выходная концентрация оказывается ниже.
Причиной этого является не скорость химической реакции (она одинакова в обоих аппаратах), а наличие или отсутствие перемешивания элементов потока. В аппарате идеального перемешивания на выходе установится концентрация, являющаяся результатом перемешивания порций вещества, находившихся внутри аппарата в течение разного времени. Некоторые порции вещества проскакивают аппарат быстро, и продолжительность реакции в таких порциях мала, а концентрация вещества А, напротив, высока. Другие порции вещества находятся внутри аппарата достаточно долго, продолжительность химической реакции велика, а остаточная концентрация А - мала.
3. Ячеечная модель потока. Согласно этой модели, реальный технологический аппарат заменяется идеализированной схемой – последовательность ячеек идеального перемешивания.
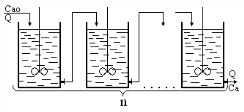 k1; 1 по А
k1; 1 по А
![]() A В
A В
![]() Пусть n=2, тогда на выходе 1-й ячейки:
Пусть n=2, тогда на выходе 1-й ячейки: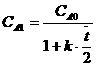
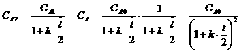
Если n ячеек, то 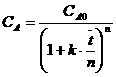
Учитывая, что  – переходим к решению для аппарата идеального вытеснения. При n=1 имеем очевидное решение для аппарата идеального перемешивания.
– переходим к решению для аппарата идеального вытеснения. При n=1 имеем очевидное решение для аппарата идеального перемешивания.
Покажем на графиках, как увеличение количества ячеек может позволить нам перейти с помощью ячеечной модели от аппарата идеального перемешивания к аппарату идеального вытеснения.

 Чтобы исключить продольное перемешивание в потоке, рабочий объём аппарата секционируют.
Чтобы исключить продольное перемешивание в потоке, рабочий объём аппарата секционируют.
Применяют также каскадирование аппаратов – последовательное соединение технологических аппаратов для выравнивания результатов химических реакций.
Моделирование кинетики в потоках химических реакций позволяет, учитывая особенности потока, рассчитать характеристики работы оборудования (выходной состав).
Моделирование явлений тепло- и массопереноса
Для технологических процессов более характерным являются гетерогенные химические реакции. В таких реакциях участвующие вещества находятся в разных фазах, собственно химическая реакция осуществляется на поверхности раздела фаз. Доставка реагентов к поверхности реагирования и отвод продуктов реакции в соответствующие фазы осуществляется в результате массопереноса.
Массоперенос
Рассмотрим взаимодействие сульфида железа, одного из компонентов медного штейна, с дутьем и флюсом в условиях конвертирования медного штейна. В первом периоде конвертирования медного штейна эта реакция является основной:
FeS(ж1) + О2(г) + SiO2(тв) → 2FeO(тв) + SiO2(ж2) + SO2(г).
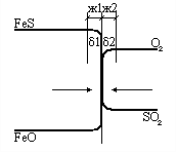 Обозначим концентрацию вещества Ся – концентрация в ядре фазы вдали от межфазной границы;
Обозначим концентрацию вещества Ся – концентрация в ядре фазы вдали от межфазной границы;
У поверхности раздела фаз концентрация этого вещества иная, обозначим ее Сп – поверхностная концентрация.
Перенос вещества из объема фазы к поверхности реагирования осуществляется в соответствии с законом Фика: ![]() ,
,
где
D – коэффициент диффузии;
δ – толщина диффузионного слоя;
(Ся-Сп) – движущая сила процесса, разность концентраций.
При заданных условиях (например, температуре), известном характере химической реакции, известных размерах частиц диффундирующих веществ D=const, определяется характером диффундирующих частиц и среды.
δ – зависит от гидродинамических особенностей процесса;
β – константа скорости диффузии;
rg – диффузионный поток – число молей вещества, доставляемых диффузией в зону реакции и отнесённое к единице поверхности.
![]()
![]() , k – константа, Сп – поверхностная концентрация.
, k – константа, Сп – поверхностная концентрация.
Справедливо для реакции 1-го порядка:
k – кинетическая константа скорости (истинная).
![]()
kCп заменим на k'Cя; известная концентрация в объёме Ся.
![]()
![]()
![]()
![]()
Величина, обратная экспериментальной константе скорости, является суммой обратных величин истинной константы и константы диффузии.
1. ![]() – наблюдается быстрая диффузия при относительно медленной химической реакции. Скорость гетерогенной реакции определяется скоростью самой медленной стадии.
– наблюдается быстрая диффузия при относительно медленной химической реакции. Скорость гетерогенной реакции определяется скоростью самой медленной стадии.
![]()
![]()
Поверхностная концентрация выравнивается с концентрацией в объёме фазы. Таким образом, диффузия доставляет вещество в зону реакции с высокой скоростью.
2. ![]() – химическая реакция быстрая при медленной диффузионной стадии. Лимитирующая стадия – диффузионная, при этом
– химическая реакция быстрая при медленной диффузионной стадии. Лимитирующая стадия – диффузионная, при этом ![]() ,
, ![]() .
.
3. ![]()
В реальных задачах моделирования определение константы диффузии и кинетической константы скорости представляет собой сложную задачу. Кинетическая константа скорости определяется экспериментально, для расчёта констант диффузии используются критериальные уравнения.
Моделирование тепловых явлений
Технологические процессы представляют собой совокупность химических реакций, сопровождающихся тепловыми эффектами. Технологические процессы происходят при высоких температурах, что требует, при составлении модели, учитывать процессы тепловыделения и теплопоглощения, а так же обмена с внутренней средой.
Технологические аппараты, как объекты моделирования могут быть отнесены к одному из трёх типов:
1. изотермические;
2. адиабатические;
3. с частичным теплообменом.
По ходу технологического процесса за счёт происходящих химических реакций либо образуется некоторое количество избыточного тепла, либо поглощается некоторое количество тепла извне. Количество выделившегося или поглощённого тепла в единицу времени зависит от скорости химической реакции.
Технологические аппараты в большинстве случаев обмениваются теплом с внешней средой, таким образом, избыточное тепло путём теплообмена отдаётся внешней среде.
Тип аппарата определяется тем, как соотносятся между собой тепловые эффекты, связанные с химической реакцией, идущей внутри аппарата и возможности теплообмена с внешней средой.
В изотермическом аппарате в единицу времени количество выделившегося и поглощённого тепла невелико:
1. скорость химической реакции невелика;
2. количество тепла, отведённое во внешнюю среду в единицу времени много больше, чем тепловой эффект внутри аппарата.
Возможности теплообмена значительно больше теплового эффекта внутри аппарата; в результате температура в аппарате приблизительно равна температуре внешней среды и остаётся постоянной.
В адиабатическом аппарате возможности внешнего теплообмена значительно уступают тепловому эффекту внутри аппарата. Такой аппарат подобен термосу- выделяющееся в ходе химической реакции тепло практически полностью расходуется на нагрев содержимого внутри аппарата, во внешнюю среду потери незначительны.
Величина теплового эффекта внутри аппарата с частичным теплообменом сопоставима с возможностями теплообмена, если в аппарате идет экзотермический процесс; часть тепла успевает рассеяться во внешнюю среду, часть расходуется на разогрев содержимого реактора, таким образом, устанавливается новая температура внутри аппарата, соответствующая тепловому балансу.
Тепловая работа аппарата с частичным теплообменом
1. Рассмотрим аппарат идеального вытеснения, в котором идет экзотермическая реакция.
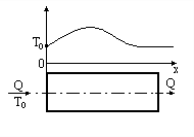 Qi –
тепловой эффект реакции.
Qi –
тепловой эффект реакции.
ri – скорость химической реак-ции.
Предполагаем, что в аппарате происходит экзотермический эффект, тогда:

1 – количество тепла, выделившегося в единицу времени;
2 – количество тепла, теряемое с поверхности аппарата во внешнюю среду;
ρ – плотность вещества в потоке;
СT – теплоёмкость вещества в потоке;
k – коэффициент теплопередачи от потока вещества к внешней среде;
f – удельная поверхность теплопередачи, отношение поверхности аппарата к его объёму;
Т0 – начальная температура на входе в аппарат;
Т – текущее значение температуры в произвольный момент времени;
Тс – температура среды;
t – время пребывания вещества в аппарате.
Приход тепла в тепловом балансе такого аппарата является суммой физического тепла вещества, поступающего в аппарат с потоком, и тепла, выделяющегося в ходе химической реакции. Расход тепла обусловлен уносом тепла веществом, покидающим аппарат с выходным потоком и потерями в окружающую среду.
Физическое тепло вещества на входе и выходе аппарата определяется его температурой, теплоемкостью и массой. Потери тепла пропорциональны разности температур в аппарате и температуры окружающей среды, а также поверхности теплообмена. Количество выделяющегося тепла зависит от теплового эффекта реакции и пропорционально скорости реакции.
Решение дифференциального уравнения теплового баланса дает функцию изменения температуры от времени пребывания вещества в аппарате. Поскольку время пребывания пропорционально расстоянию от точки входа в аппарат до произвольной точки внутри аппарата, для которой мы определяем значение температуры, можно построить профиль изменения температуры внутри аппарата.
В случае экзотермической химической реакции температура по длине аппарата изменяется от начального значения T0 (в точке входа в аппарат), которое определяется из начальных условий для решения дифференциального уравнения теплового баланса, затем возрастает до некоторого максимума, после чего убывает.
Рост температуры объясняется тем, что количество тепла, выделяющегося в начальный момент реакции, превышает возможности теплообмена с внешней средой. Избыток тепла приводит к увеличению температуры вещества в аппарате.
Скорость химической реакции в начальный момент высока, но поскольку со временем концентрация исходных веществ уменьшается (расходуются исходные вещества), количество тепла, выделяющегося за счет химической реакции в единицу времени также падает. Когда количество выделяющегося и отводимого тепла становится одинаковым, устанавливается максимальная температура в некоторой точке аппарата.
Далее количество выделяющегося тепла становится меньше, чем отводимого. Дефицит тепла в балансе приводит к снижению температуры вещества. На профиле температур в аппарате это отображается падающим участком.
На практике моделирование аппарата с частичным теплообменом такого типа позволяет проверить, не превысит ли максимальная температура допустимых значений. В таком случае необходимо изменить условия теплообмена в критической зоне аппарата, например использовать принудительное охлаждение или жидкостное охлаждение, что позволит увеличить коэффициент теплопередачи от вещества в аппарате к окружающей среде и количество отводимого тепла.
2. Работа аппарата с экзотермической химической реакцией в режиме идеального перемешивания.
Имеем химическую реакцию с выделением тепла. Количество тепла в единицу времени пропорционально скорости химической реакции:
![]()
![]() – количество тепла, поступающего с входящим потоком;
– количество тепла, поступающего с входящим потоком;
![]() – количество тепла, выносимое из аппарата выходящим потоком;
– количество тепла, выносимое из аппарата выходящим потоком;
![]() – количество тепла, выделяющегося в ходе химической реакции;
– количество тепла, выделяющегося в ходе химической реакции;
![]() – количество тепла, теряющегося в поверхности аппарата.
– количество тепла, теряющегося в поверхности аппарата.
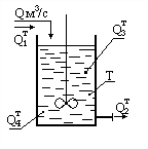
Если известны скорость химической реакции и тепловой эффект, то мы считаем всю величину Q3 известной; Q1 тоже известна; Q2 нельзя считать известной (мы не знаем Т); Q4 тоже неизвестна.
Решением этого уравнения теплового баланса является значение температуры внутри реактора. В результате моделирования мы определяем такую температуру, в зависимости от скорости химической реакции, идущей внутри аппарата. Путём итерационного расчёта значение температуры в реакторе уточняется.
Расчёт температуры позволяет судить о том, как в тепловом отношении будет работать аппарат при заданных условиях, при заданном составе вещества на входе, при заданной производительности, при заданной начальной температуре и геометрических размерах аппарата. На основании таких расчётов можно делать вывод, может ли процесс осуществляться автогенно, требуется ли дополнительный отвод тепла или необходим дополнительный источник тепла (топливо, электроэнергия и др.).
Мы познакомились с моделированием объектов на простейшем молекулярном уровне. Реальные модели процессов и объектов металлургии, как правило, значительно сложнее, они включают в себя элементы описания на более высоких уровнях: малого объема, рабочей зоны аппарата и т.д. Лишь в некоторых частных случаях можно результаты моделирования на молекулярном уровне распространить на уровень технологического аппарата в целом. Так, если химические реакции идут гомогенно, а технологический объект является аппаратом идеального перемешивания, не требуется его описания на уровне малого объема и рабочей зоны. В этом случае мы можем рассматривать аппарат в целом, как некую материальную точку в физике, поскольку, например концентрации и температуры в разных точках внутри аппарата одинаковы.
Создание модели реального процесса или технологического аппарата требует усилий, как правило, коллектива специалистов. Тем не менее, главная роль в коллективе на этапе постановки задач, на этапе получения выводов и их трактовки принадлежит к специалисту предметной области – инженеру-металлургу. Только инженер-металлург может определять такие элементы, которые могут относиться к существенным сторонам модели.
Построение математической модели технологического объекта позволяет в пределах имеющихся знаний уточнить закономерности, управляющие работой объекта. В этом смысле модель является инструментом научного познания, позволяя совершенствовать теоретические знания об объекте.
Полученная модель технологических процессов и объектов представляет собой инструмент, позволяющий прогнозировать поведение моделируемых объектов. Под прогнозированием следует понимать возможность расчета выходных характеристик технологического объекта (состава, массы полученного продукта в частности) от известных значений фиксированных входных характеристик и выбранных величин управляющих воздействий.
В таком виде модель представляет инструмент для управления технологическим объектом, позволяя ответить на вопрос: какие величины управляющих воздействий следует выбрать (и поддерживать) для того, чтобы выходные характеристики технологического объекта приняли желаемые значения.
Главное назначение модели – она предоставляет необходимые инструменты для оптимизации.


