Машиностроение и механика

Article Index
Моделирование процессов и объектов в металлургии: системный анализ
Наличие структуры или организации
Наличие интегративного качества
Классификация систем по их свойствам
Моделирование технологических процессов
Алгоритм создания модели
Структурный подход для построения математических моделей
Использование структурного подхода для составления моделей на молекулярном уровне
Матричный метод
Моделирование равновесия в системах химических реакций
Моделирование кинетики химических реакций
Скорость сложной химической реакции
Интегрирование уравнений кинетики
Численные методы интегрирования
Химические реакции в потоке вещества
Моделирование явлений тепло- и массопереноса
Моделирование тепловых явлений
Тепловая работа аппарата с частичным теплообменом
All Pages

 

Химические реакции в потоке вещества

Многие технологические аппараты работают в непрерывном режиме. Рассмотрим в качестве примера плавильную печь для переработки шихты из медных концентратов и флюсов. Схема такого аппарата приведена ниже на рисунке.

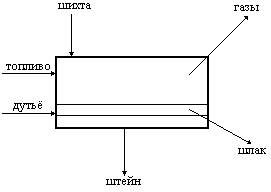Непрерывный проточный аппарат представляет собой проточный реактор, в котором осуществляется определённый набор химических реакций.

Наличие потоков вещества влияет на условия осуществления химических реакций.

Реальные потоки вещества обладают достаточно сложными свойствами:

 

 

 

 

 

 

 

 

 

· гидродинамический режим – ламинарный, турбулентный, переходный;

· число фаз – много- и однофазные.

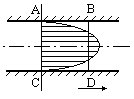
Примером является поток, движущийся по трубе. Скорость движения потока в пределах одного сечения неодинакова: наибольшее значение скорости на оси потока, а вблизи стен за счет торможения потока силами вязкости эта скорость мало отличается от нуля. Однако, если объемный расход среды потока равен Q, а площадь сечения F, нетрудно определить среднюю скорость течения потока, равную Q/F.

Q м³/c

F м²

 

 

 

Еще больше сложностей возникает при описании многофазных потоков, а реальные потоки как раз чаще всего ими и являются.

В этой связи учитывать свойства реальных потоков при создании математической модели достаточно сложно. Поэтому для создания модели аппаратов проточного типа существует несколько идеализированных моделей течения потоков.

1. Модель идеального вытеснения – такая идеализированная модель потока основана на следующих допущениях (аппаратом такого типа может быть трубчатая обжиговая печь):

· поток стационарный, объемный расход среды не меняется во времени;

dV = F·dl

 

 

 

 

 

 

· в таком потоке скорости во всех точках потока одинаковы;

· элемент объёма dV в таком потоке является замкнутой по веществу системой (не обменивается с соседними элементами);

· в потоке идеального вытеснения отсутствует продольное перемешивание;

· поперечное перемешивание в потоке тоже отсутствует.

Другое название модели идеального вытеснения – поршневой поток.

Для моделирования кинетики в случае потока идеального вытеснения вполне годится подход, применимый к системам, изолированным по веществу.

Рассмотрим реакцию первого порядка, которая проходит в аппарате идеального вытеснения.

k₁; 1 по А

A В

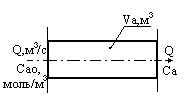Создадим модель, позволяю-щую рассчитать выходную концен-трацию А. Константа известна, поря-док первый.

– время пребывания вещества в аппарате

 

 

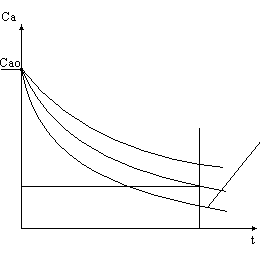
Чем больше константа скорости k,  тем быстрее концентрация стремится к концентрации в точке выхода.

В пределах аппарата идеального вытеснения концентрация вещества не остаётся постоянной – она падает от концентрации в точке входа до концентрации в точке выхода.

2. Модель идеального перемешивания (аппаратом такого типа является, например, печь КС, гидрометаллургический реактор для выщелачивания и т.п.).

Допущения:

· поток стационарный, объёмный расход вещества (Q) через аппарат должен быть постоянным;

· концентрация во всех точках аппарата идеального перемешивания одинакова.

 

 

 

 

 

 

 

 

 

Следствием второго допущения является то, что концентрация вещества в точке выхода равна концентрации внутри аппарата.

Среднее время пребывания вещества в аппарате – .

Время пребывания различных порций потока в аппарате идеального перемешивания неодинаково.

Элемент объёма в таком аппарате является открытой системой, для такого аппарата не годится подход для замкнутой системы. Для описания кинетики в этом случае используем закон вещества и рассматриваем аппарат, как единое целое, концентрация во всех точках одинакова. На основании закона сохранения вещества запишем уравнение материального баланса для всего аппарата в целом (в единицу времени):

Приход – Расход = 0

Пусть в условиях аппарата идеального перемешивания происходит реакция разложения первого порядка:

k₁; 1 по А

A В

Материальный баланс по веществу А будет суммой составляющих:

 

где:

1 слагаемое – число молей вещества А, вносимое потоком в единицу времени;

2 слагаемое– унос вещества из аппарата в единицу времени;

3 слагаемое– масса вещества, израсходованного в химической реакции. Разделим обе части уравнения на величину объемного расхода Q≠0:

, откуда

.

Создадим для химических реакций одинаковые условия в том и другом аппарате (одинаковая температура, k₁=k₂). Допустим, что при определённой температуре  k₁=k₂=1. зададим С_А0 = 1 моль/м³. Vа = 1м³, Q₁ = Q₂ = 1м³/с. Тогда:

.

Удивительно то, что результат одной и той же химической реакции оказывается в разных аппаратах разным. Более эффективным является аппарат идеального вытеснения, в котором выходная концентрация оказывается ниже.

Причиной этого является не скорость химической реакции (она одинакова в обоих аппаратах), а наличие или отсутствие перемешивания элементов потока. В аппарате идеального перемешивания на выходе установится концентрация, являющаяся результатом перемешивания порций вещества, находившихся внутри аппарата в течение разного времени. Некоторые порции вещества проскакивают аппарат быстро, и продолжительность реакции в таких порциях мала, а концентрация вещества А, напротив, высока. Другие порции вещества находятся внутри аппарата достаточно долго, продолжительность химической реакции велика, а остаточная концентрация А - мала.

3. Ячеечная модель потока. Согласно этой модели, реальный технологический аппарат заменяется идеализированной схемой – последовательность ячеек идеального перемешивания.

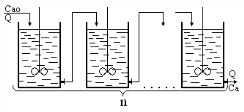k₁; 1 по А

A В

Пусть n=2, тогда на выходе 1-й ячейки: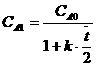

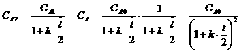
Если n ячеек, то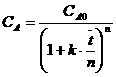

 

 

Учитывая, что – переходим к решению для аппарата идеального вытеснения. При n=1 имеем очевидное решение для аппарата идеального перемешивания.

 

 

 

 

Покажем на графиках, как увеличение количества ячеек может позволить нам перейти с помощью ячеечной модели от аппарата идеального перемешивания к аппарату идеального вытеснения.

Чтобы исключить продольное перемешивание в потоке, рабочий объём аппарата секционируют.

Применяют также каскадирование аппаратов – последовательное соединение технологических аппаратов для выравнивания результатов химических реакций.

 

 

 

 

 

 

 

Моделирование кинетики в потоках химических реакций позволяет, учитывая особенности потока, рассчитать характеристики работы оборудования (выходной состав).