Интегрирование уравнений кинетики
Пусть идет химическая реакция разложения вещества А, в результате которой образуется вещество В. Экспериментально установлено, что она имеет первый порядок по концентрации А, а значение константы скорости для условий ее осуществления равно k. Это отображено на схеме реакции ниже.
k; 1 по А
A В.
Скорость реакции равна ra = –kCA, или
.
Определим начальные условия для решения дифференциального уравнения кинетики. Будем считать, что в начальный момент реакции нам известна концентрация вещества А, обозначим ее как САо. Запишем начальные условия в виде 
. Проинтегрируем полученное уравнение, используя интегралы с подстановкой пределов. Пределы интегрирования определяются из начальных условий: когда время равно нулю, концентрация А равна начальной, в произвольный момент t концентрация равна СА:
.
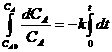В результате интегрирования имеем:
,
заменяя разность логарифмов логарифмом частного имеем далее:
,
проводя потенцирование получим:
.
После всех преобразований решение дифференциального уравнения представляет собой экспоненциальную убывающую функцию:
.
Проверим, не противоречит ли полученное решение условиям нашей задачи. При t=0, т.е. в момент начала химической реакции СA=CA0, поскольку экспонента обращается в единицу. Действительно, в начальный момент концентрация вещества А равна начальной. При t→∞ экспонента с отрицательным показателем стремится по величине к нулю. За бесконечно большое время вследствие химической реакции все вещество разлагается и образует В.