Машиностроение и механика

Article Index
Экономика отрасли
Размещение отраслей промышленности
Принципы организации отраслевой экономики
Индекс концентрации
Специализация и кооперирование в промышленности
Комбинирование в промышленности
Доминирующая фирма
Структура рынка
Барьеры входа на рынок
Конкуренция
Несовершенная конкуренция
Показатели монопольной власти
Поведение фирм на различных рынках
Условие прекращения производства товара
Парадокс Бертрана
Регулируемая монополия
All Pages

Условие прекращения производства товара

 

Если цена равна минимуму АС, фирма не получает экономической прибыли.

В условиях СК фирма, максимизирующая прибыль, может контролировать только объем выпуска, учитывая вид своей функции издержек (то есть АС) и величину цены, заданной рынком.

Специфическое условие на рынке СК: Р=MR=MC в точке равновесия.

Стратегии ценообразования в условиях СК:

1) Стратегия случайного снижения цен.

Суть: цена чуть-чуть завышается относительно рыночной, а затем понижается.

2) Стратегия сигнализирования ценами.

Суть: потребитель не может получить информацию о качестве товара; немного меняя цену, фирма сигнализирует о том, что качество ее товара лучше.

3) Стратегия цен на наборы товаров/услуг.

Суть: если потребитель купит один вид товара, то цена будет достаточно высокой, но, покупая товар в наборе с другим, потребитель будет брать его по более низкой цене.

Олигополия Курно — экономическая модель рыночной конкуренции. Названа в честь сформулировавшего ее французского экономиста А.Курно (1801-1877).

Основные положения модели:

• На рынке действует фиксированное число N > 1 фирм, выпускающих экономическое благо одного наименования;
• Вход на рынок новых фирм и выход из него отсутствуют;
• Фирмы обладают рыночной властью. Замечание: сам Курно не знал, что такое рыночная власть. Этот термин появился позднее;
• Фирмы конкурируют, одновременно выбирая объемы выпуска;
• Фирмы максимизируют свою прибыль и действуют без кооперации. Последнее замечание просто повторяет предыдущий пункт.

Общее количество фирм на рынке N предполагается известным всем участникам. Каждая фирма, принимая свое решение, считает выпуск остальных фирм заданным параметром (константой). Функции издержек фирм c_i(q_i) могут быть различны и также предполагаются известными всем участникам.

Функция спроса представляет собой убывающую функцию от цены блага. Цена блага задана как цена равновесия отраслевого рынка (величина отраслевого предложения равна величине спроса на данное экономическое благо при одной и той же цене). --Andrew A. Zimin 09:03, 5 декабря 2009 (UTC)

Рассмотрим модель с двумя фирмами (дуополию). Для определения равновесной цены вычислим наилучшие ответы каждой из фирм.

Прибыль i-й фирмы имеет вид:

Π_i = P(q₁ + q₂).q_i − C_i(q_i).

Ее наилучшим ответом является объем выпуска q_i, максимизирующий прибыль Π_i при заданном объеме выпуска другой фирмы . Производная Π_i по переменной q_i имеет вид:

Приравнивая ее к нулю, получим:

Значения q_i, удовлетворяющие данному условию, являются наилучшими ответами фирмы i. Равновесие в данной модели достигается, если q₁ является наилучшим ответом на q₂, а q₂ - наилучшим ответом на q₁.

Пусть обратная функция спроса имеет вид: P(q₁ + q₂) = a − (q₁ + q₂), а издержки фирмы i C_i(q_i) таковы, что 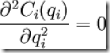, 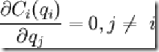. Тогда прибыль фирмы i составит:

Решение задачи максимизации имеет вид:

Таким образом, задача фирмы 1:

Из симметрии рассматриваемой системы:

Полученные выражения представляют собой функции наилучших ответов. В равновесии Нэша обе фирмы будут придерживаться стратегий, являющихся решениями пары этих уравнений. Подставляя q₂ в наилучший ответ фирмы 1, получим:

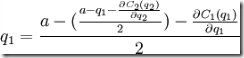
Равновесием Нэша в этой системе являются объемы выпуска (q₁ * ,q₂ * ), а равновесная рыночная цена будет представлять собой величину P(q₁ + q₂) = a − (q₁ + q₂).