Машиностроение и механика

Article Index
Детали машин: сварные, заклепочные, резьбовые соединения
Расчет сварных соединений при осевом нагружении
Рекомендации по конструированию сварных соединений встык и внахлест
Заклепочные соединения
Достоинства, недостатки и применение заклепочных соединений
Краткие сведения о материалах заклепочных соединений
Расчет на прочность элементов заклепочного шва
Допускаемые напряжения для заклепочных соединений
Резьбовые соединения
Методы изготовления резьбы
Стандартные крепежные детали
Инструмент для завинчивания и отвинчивания
Момент завинчивания, КПД и условие самоторможения
Виды повреждений резьбовых соединений
Расчет резьбовых соединений при различных случаях нагружения
Расчет групповых болтовых соединений
Расчет по условию нераскрытия стыка
Порядок проектирования резьбовых соединений
All Pages

Расчет по условию нераскрытия стыка

До приложения нагрузки F затяжка создает в стыке напряжения смятия

, (4.47)

которые принимаем равномерно распределенными по стыку. В формуле (4.47) F_3am усилие затяжки на один болт, z – число болтов, А_ст – площадь стыка. Сила F₁ растягивает болты и уменьшает на

. (4.48)

В этой формуле F₁(l – ) – часть внешней нагрузки, которая идет на разгрузку стыка (формула 4.32). В подобных соединениях значение мало. Упрощая решение, принимаем = 0, что идет в запас по условию нераскрытия стыка. При этом условии, считаем осью поворота ось симметрии стыка. Напряжения в стыке под действием момента М изменяются в соответствии с эпюрой, аналогичной эпюре напряжений при изгибе.

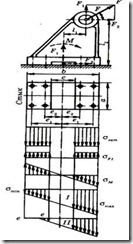
Рисунок 4.35 – Соединение под действием отрывающей силы и момента

Пренебрегая значением χ так же, как при определении _F1, приближенно запишем

, (4.49)

где W_cm – момент сопротивления изгибу, который определяется для площади стыка.

Складывая все напряжения, получим суммарную эпюру на которой

– минимальное напряжение в стыке,

– максимальное напряжение в стыке. (4.50)

В этих формулах за положительные приняты напряжения затяжки _зат. Вариант I показывает нераскрытие стыка и принимается как расчетный. Вариант II свидетельствует о раскрытии стыка на участке ее, так как напряжения здесь равны нулю, что недопустимо.

По условию нераскрытия стыка

σ_min > 0 или σ_зат > σ_F1 + σ_М или (4.51)

где К 1,3. ..2 – коэффициент запаса по нераскрытию стыка. По условию (4.51) определяют _зат и затем из формулы (4.47) находят F_заm.

В тех случаях, когда материал основания по прочности меньше, чем материал болта, необходимо проверять условие прочности основания по максимальным напряжениям смятия . Если это условие не удовлетворяется, изменяют размеры стыка.

Расчет по условию отсутствия сдвига деталей в стыке. Этот расчет выполняют как проверочный. Сила F₂ уравновешивается силами трения в стыке. Детали остаются неподвижными, если сила трения в стыке больше F₂ или

, (4.52)

где – коэффициент трения в стыке, можно принимать: = 0,3 – 0, 35 – сталь (чугун) по бетону; f = 0,15 – 0, 20 – сталь по чугуну (по стали); z – число болтов.

В формуле (4.52) не учитывается действие момента М, так как он не сдвигает детали и не изменяет суммарного значения сил трения в стыке. Если условие не выполняется, то это значит, что условие (4.51) нераскрытия стыка не является главным для данного соединения и затяжку следует определять по условию (4.52) несдвигаемости деталей

(4.53)

или ставить болты без зазора.

При расчете болтов на прочность учитывают наибольшую силу затяжки F_зaт из найденных по условию (4.51) или (4.53). Внешняя нагрузка, приходящаяся на один болт от силы F₁:

, (4.54)

внешняя нагрузка от момента М определяется из равенства

M=i(F_м12e₁+F_M22e₂ +...+F_Mn2e_n),

где i – число болтов в поперечном ряду (на рисунке 4.35 i = 2); n — число поперечных рядов с одной стороны от оси поворота (на рис. 4.35 n= 2).

Силы F_м1, F_M2,... пропорциональны их расстояниям от оси поворота: и т.д.

Учитывая это, после несложных преобразований находим наиболее нагруженный болт от момента:

. (4.55)

Суммарная нагрузка

.

При известных F_3am и F_max расчетную нагрузку определяют по формуле (4.33), а прочность болта при статических нагрузках оценивают по формуле

. (4.57)

Форма стыка оказывает влияние на прочность соединения. Например, для сплошного 1 и несплошного 2 стыков, изображенных на рис. 4.36, значения площадей и моментов сопротивления изгибу равны:

; ; ;

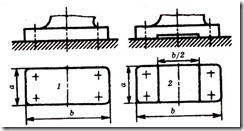
Рисунок 4.36 – Формы стыков