Машиностроение и механика

Article Index
Детали машин: сварные, заклепочные, резьбовые соединения
Расчет сварных соединений при осевом нагружении
Рекомендации по конструированию сварных соединений встык и внахлест
Заклепочные соединения
Достоинства, недостатки и применение заклепочных соединений
Краткие сведения о материалах заклепочных соединений
Расчет на прочность элементов заклепочного шва
Допускаемые напряжения для заклепочных соединений
Резьбовые соединения
Методы изготовления резьбы
Стандартные крепежные детали
Инструмент для завинчивания и отвинчивания
Момент завинчивания, КПД и условие самоторможения
Виды повреждений резьбовых соединений
Расчет резьбовых соединений при различных случаях нагружения
Расчет групповых болтовых соединений
Расчет по условию нераскрытия стыка
Порядок проектирования резьбовых соединений
All Pages

Расчет резьбовых соединений при различных случаях нагружения

Стержень винта нагружен только растягивающей силой. Этот случай встречается редко. Примером служит нарезанный участок крюка для подвешивания груза (рисунок 4.25). Опасным бывает сечение, ослабленное резьбой. Расчет сводится к определению внутреннего диаметра резьбы d₁ из условия прочности на растяжение, которое имеет вид:

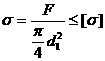, (4.16)

откуда

,

где []– допускаемое напряжение на растяжение для винта (болта);

, (4.17)

где – предел текучести материала болта; [п_T] – требуемый (допускаемый) коэффициент запаса прочности.

Для болтов из углеродистой стали принимают [п_T] = 1,5 – 3. Большие значения коэффициента запаса [п_T] принимают при невысокой точности определения величины нагрузки F или для конструкций повышенной ответственности.

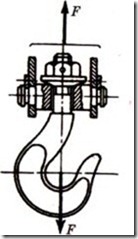
Рисунок 4.25 – Грузовой крюк под нагрузкой

Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рисунок 4.26). В этом случае стержень болта растягивается осевой силой F_gam, возникающей от затяжки болта, и закручивается моментом сил в резьбе Т_р – формула (4.7). Напряжение растяжения от силы F_gam

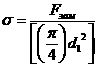. (4.18)

Напряжение кручения от момента Т_p

. (4.19)

Требуемое значение силы затяжки определяют следующим образом:

,

где А – площадь стыка деталей, приходящаяся на один болт, _см – напряжения смятия в стыке деталей, значение которого выбирают по условиям герметичности.

Прочность болта определяют по эквивалентному напряжению:

. (4.20)

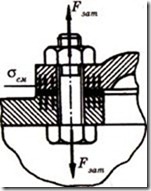
Рисунок 4.26 – Соединение под действием усилия затяжки

Практические вычисления показывают, что для стандартных метрических резьб _эк 1,3.

Рис. 4.26. Соединение под действием усилия затяжки

Это позволяет рассчитывать болты на прочность по следующей упрощенной формуле:

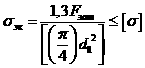, (4.21)

Рис. 4.26. Соединение под действием усилия затяжки

Рис. 4.26. Соединение под действием усилия затяжки

откуда

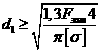, (4.22)

где [σ] – допускаемые напряжения на растяжение для винта (болта), определяемое по формуле (4.17).

Практикой установлено, что болты с резьбой, меньше М10, можно повредить при недостаточно квалифицированной затяжке. Поэтому в силовых соединениях не рекомендуют применять болты малых диаметров (меньше М8). На некоторых производствах для затяжки болтов используют специальные ключи предельного момента. Эти ключи не позволяют приложить при затяжке момент, больше установленного.

Болтовое соединение нагружено силами в плоскости стыка. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть собрана по двум вариантам.

Болт поставлен с зазором (рисунок 4.27). В этом случае болт ставится с зазором в отверстие деталей. При затяжке болта на стыке деталей возникают силы трения F, которые препятствуют относительному их сдвигу. Внешняя сила F непосредственно на болт не передается, поэтому его рассчитывают по силе затяжки F. Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей

, или , (4.23)

где i – число плоскостей стыка деталей (на рисунке 4.27 – i = 2; при соединении только двух деталей i = 1); – коэффициент трения в стыке (= 0,15 – 0,2 для сухих чугунных и стальных поверхностей); К –коэффициент запаса по сдвигу деталей (К = 1,3 – 1,5 при статической нагрузке, К = 1,8 – 2 при переменной нагрузке).

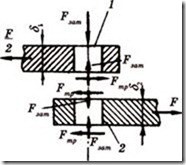
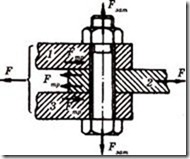
Рисунок 4.27 – Болт поставлен с зазором

Как известно при затяжке болт работает на растяжение л кручение поэтому прочность болта оценивают по эквивалентному напряжению – формула (4.21). Так как внешняя нагрузка не передается на болт, его рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.

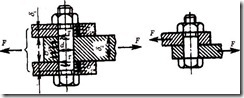
Рисунок 4.28 – Болт поставлен без зазора

Болт поставлен без зазора (рисунок 4.28). В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности данного соединения не учитывают силы трения в стыке, так как затяжка болта не контролируется. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза будет иметь вид:

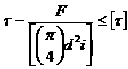, (4.24)

где i – число плоскостей среза (на рисунке 4.28, a i = 2; при соединении только двух деталей – рис. 4.28, б i = 1); [τ] – допускаемое напряжение на срез для стержня болта:

[] = (0,2 – 0,3)_т. (4.25)

Диаметр стержня болта d определяют из условия прочности на срез формула (4.24):

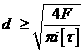. (4.26)

Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали (рисунок 4.29) трудно установить точно. Это зависит от точности размеров и форм деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рисунок 4.29, а) заменяют условной с равномерным распределением напряжений (рисунок 4.29, б).

Для средней детали (и при соединении только двух деталей)

или (4.27)

для крайних деталей

. (4.28)

Формулы (4.27) и (4.28) справедливы для болта и деталей. Из двух значений [_см] в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали. Сравнивая варианты постановки болтов с зазором и без зазора (рисунок 4.27 и 4.28), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. Так, например, приняв коэфициент трения в стыке деталей = 0,2, К = 1,5 и i = 1, из формулы (4.23) получим F_заm = 7,5F. Следовательно, расчетная нагрузка болта с зазором в 7,5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициент трения и трудности контроля затяжки работа таких сопений при сдвигающей нагрузке недостаточно надежна.

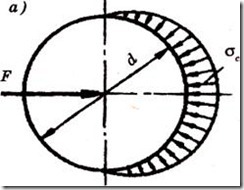
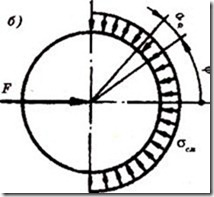
Рисунок 4.29 – Распределение напряжений смятия по цилиндрической поверхности контакта болта и детали

Болтовое соединение предварительно затянуто при сборке и гружено внешней осевой растягивающей силой. Этот случай соединения (рисунок 4.30) часто встречается в машиностроении для крепления крышек цилиндров, подшипниковых узлов и т. п. Обозначим: F_з – сила предварительной затяжки болта при сборке; F – внешняя растягивающая нагрузка, приходящаяся на один болт. Предварительная затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой.

В результате предварительной затяжки болта силой F_з (рисунок 4.30, б и рисунок 4.31) он удлинится на величину Δl_б, а детали стыка сожмутся на Δl_д (на рисунках для большей наглядности величины Δl_б и Δl_д сильно увеличены).

При действии на предварительно затянутый болт внешней растягивающей нагрузки F (рисунок 4.30, в и рисунок 4.31) болт дополнительно удлинится на величину Δl’_б, а сжатые детали частично разгрузятся и восстановят свою толщину на Δl’_д, причем, в пределах до раскрытия стыка,

Δl’_б= Δl’_д. (4.29)

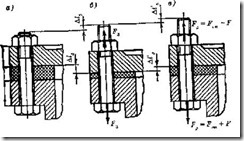Рисунок 4.30 – Схема для расчета болтового соединения:

а – болт не затянут;

б – болт затянут;

в – к затянутому болту приложена внешняя сила F

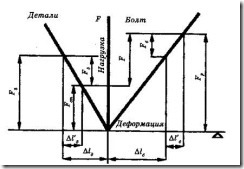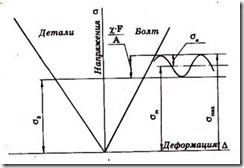
Рисунок 4.31 – Изменение нагрузки и деформации в болтовом соединении с предварительной затяжкой и последующим нагружением осевой растягивающей силой

Действие сжатых деталей на болт уменьшится и составит F_cm (рисунок 4.30, и рисунок 4.31), которое называется остаточным усилием затяжки.

В этом случае часть внешней нагрузки пошла на разгрузку стыка F_д, а оставшаяся часть внешней нагрузки пошла на догружение болта F_б. В итоге можно записать:

F_д+F_б=F. (4.30)

Известно, что деформация определяется по формуле

,

где F – нагрузка, l – длина нагружаемого участка, Е – модуль продольной упругости, А – площадь поперечного сечения, на которой действует нагрузка.

Выражение 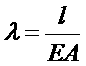– называется податливостью, тогда . Равенство (4.29) можно записать в виде: , тогда , последнее подставляем в (4.30). В результате получаем , откуда

, (4.31)

где – коэффициент внешней нагрузки, – податливость деталей, – податливость болта.

После подстановки (4.31) в (4.30) получим F_д + F = F, откуда

F_д=F-F=F(1-). (4.32)

Коэффициент внешней нагрузки показывает, какая часть внешней нагрузки F идет на догружение болта F, а оставшаяся часть

F(l-) идет на разгрузку деталей в стыке см. (4.31) и (4.32).

Полное усилие или расчетная (суммарная) нагрузка на болт F (рисунок 4.31)

. (4.33)

Условие нераскрытия стыка F_cm > 0. На рис. 4.31 видно, что

,

тогда условие нераскрытия стыка будет иметь вид F_д-F(1 – )>0 или F₃ > F(1 - ). На практике рекомендуют принимать

, (4.34)

где К_з – коэффициент запаса затяжки, тогда расчетное усилие F_р определяют по формуле:

, (4.35)

при постоянной нагрузке К_з – (1,25...2), при переменной нагрузке К_з = (2,5 – 4).

Определение податливости болта и деталей. В простейшем случае при болтах постоянного сечения и однородных деталях (рис. 4.32)

;, (4.36)

где Е_б и Е_д – модули упругости материалов болта и деталей; А_б и А_д – площади сечения болта и деталей; l_б – длина болта, участвующая в деформации; l_д = δ₁ + δ ₂ – суммарная толщина деталей; приближенно l_б= l_д.

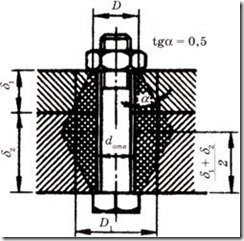
Рисунок 4.32 – Конусы давления

В формуле (4.36) под расчетной площадью А_д принимают площадь только той части деталей, которая участвует в деформации от затяжки болта. Условное определение этой площади в простейшем случае изображено на рисунке 4.32. Здесь полагают, что деформации от гайки и головки болта распространяются в глубь деталей по конусам с углом 30°, или tg = 0,5. Приравнивая объем этих конусов к объему эквивалентного цилиндра, находим его наружный диаметр D₁ и площадь цилиндра А_д

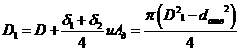. (4.37)

Опыт расчетов и эксплуатации конструкций показывает, что коэффициент обычно небольшой.

При приближенных расчетах принимают:

1. Для соединений стальных и чугунных деталей, без упругих прокладок = 0,2 – 0,3.

2.Для соединений стальных и чугунных деталей с упругими прокладками (асбест, поронит, резина и др.) = 0,4 – 0,5.

3. В уточненных расчетах определяют значения _д и _б, а затем .

При проектировании резьбовых соединений основным правилом является: жесткие фланцы – податливые болты.

Если болт затянут предварительно, до приложения внешней нагрузки, то расчетное усилие на болт с учетом влияния кручения при затяжке

. (4.38)

Прочность болта при переменных нагрузках. Наиболее характерным случаем действия переменных внешних нагрузок на болтовые соединения является действие нагрузок, изменяющихся от 0 до F (по отнулевому циклу).

Рисунок 4.33 – Диаграмма изменения напряжений при переменной нагрузке

Переменная нагрузка F распределяется между болтом и затянутым стыком, причем на винт приходится доля, равная (см. диаграмму на рис.

Амплитуда напряжения болта

, (4.39)

где А_б – площадь опасного сечения болта.

Среднее напряжение

, (4.40)

где _з – напряжения затяжки.

Максимальное напряжение

.

Опыт эксплуатации резьбовых соединений, подверженных действию переменных нагрузок, а также испытания соединений на усталость показывают целесообразность значительной начальной затяжки соединений для болтов из углеродистых сталей равной (0,6 – 0,7)_т, а из легированных сталей – (0,4 – 0,6)_т.

Затяжка увеличивает усталостную прочность болтов (так как уменьшает переменную составляющую напряжений в болтах) и соединяемых деталей (так как уменьшает микросдвиги). Следует учитывать, что напряжения затяжки при эксплуатации могут несколько снизиться вследствие обмятия микронеровностей на стыках и релаксации напряжений в болтах.

В расчетах проверяют запас прочности по амплитудам и максимальным напряжениям.

Запас прочности по амплитудам определяют как отношение предельной амплитуды (приближенно принятой равной пределу выносливости винта при симметричном цикле нагружения) _ал = к действующей амплитуде напряжений :

. (4.41)

Значения эффективного коэффициента концентрации напряжений К для метрической резьбы соединений винт–гайка из углеродистых сталей принимают равными 4 – 6, из легированных сталей с _в < 130 МПа 5,5 – 7,5; большие значения принимают для винтов из более прочных материалов и термически обработанных до изготовления резьбы.

Запас прочности по максимальным напряжениям определяют приближенно как отношение предельного напряжения _пр к действующему максимальному напряжению в болте . Обычно этот расчет сводится к расчету на статическую прочность, тогда _пр =_т и

. (4.42)

Расчет болтов, подверженных переменной нагрузке, выполняют в форме проверочного. Значение коэффициента запаса прочности по амплитудам должно быть больше или равно 2,5, обычно п_а = 2,5 – 4. Значение коэффициента запаса прочности по максимальным напряжениям должно быть больше или равно 1,25.