Машиностроение и механика

Article Index
Детали машин: сварные, заклепочные, резьбовые соединения
Расчет сварных соединений при осевом нагружении
Рекомендации по конструированию сварных соединений встык и внахлест
Заклепочные соединения
Достоинства, недостатки и применение заклепочных соединений
Краткие сведения о материалах заклепочных соединений
Расчет на прочность элементов заклепочного шва
Допускаемые напряжения для заклепочных соединений
Резьбовые соединения
Методы изготовления резьбы
Стандартные крепежные детали
Инструмент для завинчивания и отвинчивания
Момент завинчивания, КПД и условие самоторможения
Виды повреждений резьбовых соединений
Расчет резьбовых соединений при различных случаях нагружения
Расчет групповых болтовых соединений
Расчет по условию нераскрытия стыка
Порядок проектирования резьбовых соединений
All Pages

Момент завинчивания, КПД и условие самоторможения

Соотношения между силами и моментом завинчивания в резьбовом соединении. Вначале изучим зависимости для прямоугольной резьбы, а потом распространим их и на другие типы резьб.

При рассмотрении сил в винтовой паре удобно резьбу развернуть по среднему диаметру d₂ в наклонную плоскость, а гайку заменить ползуном (рис. 4.22, а). Сила взаимодействия наклонной плоскости с ползуном при относительном движении представляет собой равнодействующую нормальной силы и силы трения. Следовательно, эта сила наклонена к нормали п под углом трения ф. В результате разложения силы получаем

, (4.2)

где F_t – движущая окружная сила; F – осевая сила на винте; – угол подъема винтовой линии резьбы.

Окружная сила трения в треугольной резьбе больше, чем в прямоугольной резьбе. Соотношение окружных сил трения в прямоугольной и треугольной резьбах удобно рассмотреть на моделях с кольцевыми витками, приняв угол подъема резьбы, равной нулю (рисунок 4.22, б).

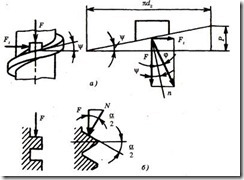
Рисунок 4.22 – Силы взаимодействия между винтом и гайкой

Окружная сила трения для витка прямоугольного профиля Для витка треугольного профиля F₁=Nf

Для витка треугольного профиля

, (4.3)

где ; – угол профиля резьбы, откуда приведенный коэффициент трения

. (4.4)

Таким образом, силу трения в треугольной резьбе можно определить так же, как в прямоугольной, только вместо действительного коэффициента трения надо пользоваться приведенным, равным действительному, деленному на cos(a/2).

Аналогичное соотношение имеет место между углами трения:

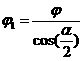. (4.5)

Для нормальной метрической резьбы угол (сс/2)=30°, а следовательно,

f₁ ≈ 1,15

и = 1,15 (здесь – приведенный угол трения).

Для определения движущей окружной силы в треугольной резьбе можно пользоваться выведенной формулой для прямоугольной резьбы, подставив вместо действительного приведенный угол трения.

Момент завинчивания гайки или винта с головкой

Т_зав= Т_р+Т_т, (4.6)

где Т_р – момент в резьбе; Т_T – момент трения на торце гайки или головки винта. Момент в резьбе

. (4.7)

Опорную поверхность гайки и головки принимают кольцевой с наружным диаметром, равным размеру под ключ D₁ и внутренним диаметром, равным диаметру отверстия под винт d₀.

Момент трения на торце гайки или головки

, (4.8)

где ; – коэффициент трения на торце гайки.

Эта удобная для расчета зависимость основана на предположении, что давление на торце гайки увеличивается с уменьшением радиуса. Увеличение давления связано с упругим деформированием тела гайки и уменьшенными путями трения на малых радиусах при завинчивании и отвинчивании.

Момент на торце гайки или головки винта составляет около 50% всего момента затяжки.

Подставив полученные выражения Т_р и Т_т в формулу для момента завинчивания, получим окончательно

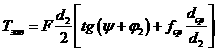. (4.9)

При отвинчивании гайки окружная сила F_t и силы трения меняют направление на противоположное. При этом получим F_t = Ftg().

Момент отвинчивания с учетом трения на торце гайки, по аналогии с моментом завинчивания будет иметь вид

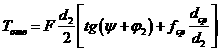. (4.10)

Полученные зависимости позволяют отметить:

По формуле (4.9) можно подсчитать отношение осевой силы винта F к силе F, приложенной на ручке ключа, , которое дает выигрыш в силе. Для стандартных метрических резьб при стандартной длине ключа

l ≈ 15d

и = 0,15 = 70 – 80 .

Стержень винта не только растягивается силой F, но и закручивается моментом Т_р.

Условие самоторможения можно записать в виде Т_отв > 0, где Т_отв определяется по формуле (4.10). Рассматривая самоторможение только в резьбе без учета трения на торце гайки, получим tg( ) > 0 или

ψ < φ₁. (4.11)

Для крепежных резьб значение угла подъема лежит в пределах 2°30' – 3°30', а угол трения изменяется в пределах 6° (при ) – 16º (при f 0,3). Таким образом, все крепежные резьбы – самотормозящие. Резьбы для ходовых винтов выполняют как самотормозящие, так и несамотормозящие.

Приведенные выше значения коэффициента трения, свидетельствующие о существенных запасах самоторможения, справедливы только при статических нагрузках. При динамических и вибрационных нагрузках вследствие взаимных микросмещений поверхностей трения коэффициент трения существенно снижается и условие самоторможения нарушается. Происходит самоотвинчивание во избежание которого применяют специальные стопорные устройства (см. Специальные способы стопорения резьбовых соединений).

КПД винтовой пары определяется отношением работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов , в котором Т_зав определяется по формуле (4.9), а Т'_зав – по той же формуле, но при и :

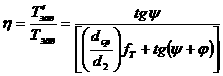. (4.12)

Учитывая потери только в резьбе (Т_T = 0), найдем КПД только винтовой пары:

. (4.13)

Формула (4.13) позволяет сделать вывод, что возрастает с увеличением и уменьшением .

Распределение осевой нагрузки виткам резьбы. При нагружении осевая сила распределяется между витками неравномерно. Неравномерность распределения сил по виткам усугубляется тем, что витки на наиболее растянутой части винта сопрягаются с витками, расположенными в наиболее сжатой части гайки. Задача о распределении нагрузки по виткам статически неопределима. Распределение сил между витками резьбы, полученное Н.Е. Жуковским для гайки с десятью витками, показано на рисунке 4.23. На первый, наиболее нагруженный, виток приходится около 1/3 общей силы на винт, а на десятый виток – менее 1/100 общей силы. Деформации в резьбе, связанные с погрешностями профиля, контактные деформации несколько снижают нагрузку на первый виток резьбы. При такой большой неравномерности распределения осевой силы по виткам большое увеличение высоты гайки оказываются бесполезным в связи с опасностью последовательного разрушения витков.