Длина ламинарного газового факела
Идеальная картина поверхностного горения газа получается при направлении ламинарной струи газа вертикально вверх, так как при другом направлении ламинарной струи из-за действия подъемной силы факел получается искривленным. Под высотой или иначе длиной ламинарного факела понимают расстояние от сопла до точки, где оканчивается процесс горения.
При сжигании однородных стехиометрических смесей в ламинарном факеле общая скорость процесса горения определяется ходом процесса перемешивания продуктов сгорания со свежей горючей смесью при проникновении некоторой части продуктов сгорания из фронта пламени навстречу течению горючей смеси. Этот процесс сопровождается передачей тепла теплопроводностью к новым порциям смеси и зажиганием их.
При сжигании заранее подготовленной стехиометрической смеси горючего газа с воздухом в ламинарной струе фронт пламени локализуется в очень тонком поверхностном слое, в результате чего горящая струя приобретает форму конуса, остроконечная вершина которого находится в том месте, где оканчивается процесс горения. Длина факела по данным В. А. Михельсона, равна
,
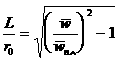где `w - средняя скорость истечения смеси из сопла, м/с;
`wпл = `w×cosa - средняя скорость распространения пламени (здесь a - угол между направлением движения смеси и нормалью к фронту горения;
r0 - радиус сопла, из которого истекает стехиометрическая смесь, м.
При `wпл > `w квадрат безразмерной длины факела (Lфак/d0)2 равен отрицательной величине. Практически это означает, что процесс горения проникает внутрь самого сопла. Поэтому длина факела по уравнению В. А. Михельсона получается мнимой величиной.
Ламинарно-диффузионный факел
При ламинарно-диффузионном факеле топливо и воздух подают раздельно. Топливо и кислород, чтобы перемешаться и вступить в реакцию должны диффундировать навстречу друг к другу через слой продуктов сгорания.
Согласно теории Бурке и Шумана, положение фронта диффузионного пламени определяется как геометрическое место точек, в которых отношение количества горючего газа, диффундирующего наружу, к количеству кислорода, диффундирующего внутрь, удовлетворяет стехиометрическому уравнению полного сгорания горючего газа. Таким образом, в пламени в зоне окисления не может существовать несгоревшее топливо, а в топливной зоне - непрореагировавший кислород, если только в самой струе горючего газа не содержался первичный кислород.
Далее принимали, что скорость химических реакций горения на много больше скорости диффузии. Это означает, что горение локализовано в тонком слое между топливом и окислителем, а скорость распространения пламени определяется в первую очередь скоростями диффузии молекул топлива и окислителя через слой продуктов сгорания в зону горения.
Ниже приведена формула для расчета длины ламинарно-диффузионного факела, в основу которой положены предпосылки Бурке и Шумана
Lф = 
,
где Vc - объемный расход газа через сопло, м3/с;
u и Dv - коэффициенты кинематической вязкости и диффузии, м2/с;
k0 - размерная постоянная, определяемая из опыта, с/м3 (k0 » 0,5);
- молярная концентрация топлива в стехиометрической смеси,
здесь us - стехиометрический расход воздуха, необходимый для сжигания 1 м3 газа, м3/м3;
- начальная молярная концентрация топлива в смеси с воздухом,
здесь u0 - объемное количество воздуха, предварительно перемешенного с 1 м3 газа, м3/м3.
Для конкретных расчетов более удобно, задаваясь длиной факела определять секундный расход газа.
Из рассмотренного уравнения можно сделать следующие выводы:
1. Длина ламинарно-диффузионного факела в сильной мере зависит от расхода газа через сопло.
2. На длину ламинарно-диффузионного факела существенное влияние оказывает произведение u×Dv .
3. Чем больше стехиометрический расход воздуха us , тем длиннее факел.