Метод координатного спуска
В этом методе направление поиска совпадает с направлением координат (осями факторов). На любом шаге решения можно менять только один фактор, а все остальные остаются без изменения.
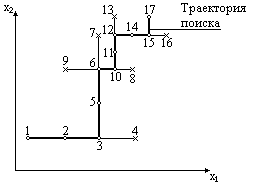
Поиск решения начинается в начальной точке 1 (см. рис.), где вычисляется значение целевой функции. Затем начинаем движение по пространству переменных в пределах области допустимых решений. Это означает, что увеличив координату на величину начального шага вдоль х1, и оставив без изменения х2, мы переместимся в новую точку 2. Вычислим значение целевой функции в этой точке и сравним его с предыдущим. Если при поиске минимума значение функции в точке 2 меньше, чем в точке 1, то такой шаг следует считать удачным. В этом случае поиск продолжается в выбранном направлении. Двигаясь вдоль х1 и вычисляя на каждом шаге значение целевой функции, мы рано или поздно можем убедиться в том, что последующее значение станет больше предыдущего. Такой шаг является неудачным. Если очередной шаг решения оказался неудачным, направление поиска изменяется. Для этого координату последней удачной точки по х1 фиксируют, и начинают движение в направлении х2, используя величину начального шага. Вблизи области минимума движение начальным шагом во всех разрешенных направлениях не приводит к улучшению значения целевой функции. При этом одна из точек окажется наилучшей, в ней значение целевой функции наименьшее. Однако задача еще не решена, поскольку величина начального шага выбирается заведомо больше интересующей нас точности решения. Фактически задача пришла к исходной – имеется начальная точка поиска (наилучшая), и требуется путем движения по пространству переменных найти такую точку, в которой значение целевой функции еще меньше. Для этого последующий поиск надо проводить, двигаясь шагом уменьшенной величины. Такой шаг получают делением начального шага на коэффициент сокращения шага, обычно его выбирают равным от 2 до 5. Разделив начальные шаги на соответствующие коэффициенты сокращения продолжают поиск, пока одна из точек вновь не станет наилучшей и т.д. Критерием завершения поиска является достижение заданной точности решения.