Решение задач линейного программирования
Рассмотрим решение задачи линейного программирования графическим методом на следующем при мере.
Имеется предприятие, производящее 2 продукта: А и В. Продукты отличаются по цене: продукт А имеет цену 3 у.е. за тонну, продукт В – 5 у.е. за тонну. Кроме того, производство одной тонны продукта А требует 3, а продукта В -9 единиц сырья. Запас сырья на предприятии ограничен и составляет 75 единиц. Общее количество продуктов А и В не должно превышать 10 тонн, что обеспечит стабильность цен при их продаже. Производство более дешевого продукта А не может превышать производство более дорогого продукта В более чем на 3 тонны. Расход сырья на производство не может превышать имеющегося запаса в 75 единиц.
С учетом этого сформулируем математически условия задачи. Обозначим как х1 массу продукта А, а х2 – массу продукта В соответственно. Тогда целевая функция L будет определяться следующим выражением:
|
|
А |
В |
|
Цена |
3 |
5 |
|
Выпуск, т |
Х1 |
Х2 |
L = 3x1 + 5x2 → max.
Требуется определить такие х1 и х2, при которых эта функция максимальна.
Из условий задачи вытекает ряд ограничений:
![]() x1 ≥ 0
x1 ≥ 0
x2 ≥ 0
3x1 + 9x2 ≤ 75
x1 + x2 ≤ 10
x1 – x2 ≤3
Используем имеющиеся ограничения и вид целевой функции для поиска решения графическим методом.
Поскольку наша задача содержит две неизвестных величины, отведем для них две оси в декартовой системе координат. Обе оси лежат в одной плоскости, которая в данном случае является пространством переменных.
Первое ограничение задачи x1 ≥ 0 делит пространство переменных на две половины, одна из которых является разрешенным, а другая – запрещенным полупространством. Второе ограничение x2 ≥ 0 также отсекает от пространства переменных разрешенное полупространство. Оба первых ограничения совместны в первом квадранте декартовой плоскости. Заметим, что и на осях переменных ограничения не нарушаются, поскольку ограничения являются нестрогими неравенствами. Разрешенное полупространство покажем штриховкой.
Третье ограничение задачи 3x1 + 9x2 ≤ 75 в предельном виде можно рассматривать как уравнение прямой в выбранной системе координат: 3x1 + 9x2 =75, или х2= -1/3х1+25. Положение этой прямой показано ниже на рисунке. Разрешенное полупространство расположено ниже прямой.
Используя оставшиеся ограничения, проведем соответствующие им прямые и покажем разрешенное полупространство для каждой из них.
В результате всех построений на пространстве переменных образуется область, внутри которой и на границах которой совместно выполняются все ограничения данной задачи. Это область 0ACEG, имеющая вид пятиугольника, называется областью допустимых решений данной задачи. Особенности области допустимых решений (ОДР) вытекают из ограничений задачи.
Любая точка внутри и на границах ОДР, а также на пересечении границ, т.е. в вершинах ОДР, является допустимым решением. Также очевидно, что число допустимых решений бесконечно велико. Нас же интересует оптимальное решение, т.е. такое, при котором целевая функция нашей задачи обращается в максимум.
Вторым этапом решения и является поиск оптимального решения на области допустимых решений. Для этого воспользуемся выражением для целевой функции
L = 3x1 + 5x2. Зададим L произвольное значение, пусть например L=15. Последнее означает, что мы определили в трехмерном пространстве, имеющем ось для отображения целевой функции, некую плоскость, для любой точки которой значение целевой функции неизменно и равно 15, независимо от значений x1 и х2. С другой стороны, выражение L = 3x1 + 5x2 определяет положение плоскости целевой функции в выбранной системе координат. Плоскость целевой функции проходит через начало координат и наклонена к по отношению к осям переменных. Этот наклон тем больше, чем больше коэффициент при соответствующей переменной.
Выражение 3x1 + 5x2=15 означает, что плоскости в пространстве пересекаются. Линия пересечения плоскости постоянного уровня и плоскости целевой функции есть прямая, проекция ее на пространство переменных также является прямой, которая называется прямой опорного решения (ПОР).
В нашей задаче положение ПОР соответствует уравнению прямой х2=-3/5х1+3.
Она отсекает на оси х1 отрезок, равный 5, а на оси х2 – 3 единицам. Возрастание целевой функции происходит при увеличении х1 и х2, что показано стрелками на ПОР на рисунке.
Значение 15 мы выбрали произвольно. Если задать большее значение, линия пересечения плоскости целевой функции и плоскости постоянного уровня целевой функции переместится в пространстве параллельно самой себе, а ее проекция переместится параллельно ПОР вправо и вверх.
Нетрудно заметить, что наиболее далеко отстоящей точкой от ПОР является вершина области допустимых решений С, в которой и будет наибольшее значение целевой функции L. Эта вершина области и будет оптимальным решением нашей задачи.
Положение вершины С определяется решением системы уравнений:
х1+х2=10
3х1+9х2=75,
что дает координаты С(2,5;7,5). Значение целевой функции при этом равно 45.
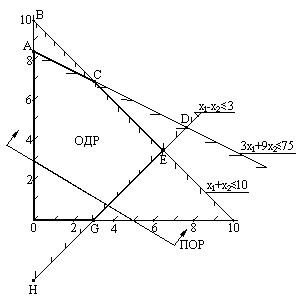
![]() ПОР –прямая опорного решения.
ПОР –прямая опорного решения.
3x1 + 9x2 = 75
x1 + x2 = 10
x1 = 2,5, x2 = 7,5
L = 45
Графический метод не может быть использован, если число переменных в задаче больше двух, поскольку пространство переменных становится многомерным, а задача лишается наглядного образа. Для решения таких задач линейного программирования (а реальные задачи могут содержать сотни переменных) используются иные методы, например симплекс-метод и метод искусственного базиса.
Алгоритмы методов решения задач линейного программирования известны, исследованы математиками с точки зрения сходимости и наличия решения. На базе имеющихся алгоритмов созданы программы, входящие в пакеты прикладных программ общего назначения и проблемно-ориентированных. В частности, решение задач линейного программирования может быть достигнуто при использовании электронных таблиц Microsoft Excel или математического пакета MathCAD. Наличие таких инструментов упрощает получение решения. Основная сложность состоит в корректной постановке задачи, а также в интерпретации и проверке полученных результатов.


