Классификация оптимизационных задач
Все множество оптимизационных задач можно разделить на несколько классов по следующим признакам:
1. Вид экстремума целевой функции. Нас может интересовать поиск максимума или минимума целевой функции. Как известно, переход от поиска минимума к поиску максимума не представляет труда: минимум функции y=f(x) достигается при тех же условиях, что и максимум функции –y=–f(x). Таким образом, для смены знака экстремума достаточно целевую функцию умножить на минус единицу. Пример пояснен на рисунке.
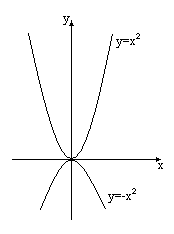
2. Число критериев оптимальности. По этому признаку все множество задач оптимизации можно разделить на два подмножества:
а) однокритериальные задачи;
б) многокритериальные задачи.
В первом случае в задаче может быть сформулирован единственный критерий оптимальности. При необходимости он может быть получен из нескольких частных критериев оптимальности одним из ранее описанных методов (аддитивный, мультипликативный).
Во втором случае в задаче по принципиальным соображениям нет единственного критерия оптимальности. Решение такой задачи часто бывает неоднозначным, а математические методы решения разработаны хуже, чем для однокритериальных задач. По этой причине всегда имеет смысл попытаться построить единственный критерий оптимальности путем свертки нескольких частных критериев.
3. По числу оптимизирующих факторов. Здесь также можно выделить два подмножества:
а) однофакторные задачи;
б) многофакторные задачи.
В первом случае в задаче имеется единственный оптимизирующий фактор (единственное управляющее воздействие не объект, которое мы можем изменять в заданных пределах). Математически это означает, что целевая функция зависит от величины единственного своего аргумента.
Во втором случае целевая функция зависит от нескольких (двух и более) аргументов. Имеется два и более управляющих воздействия, изменяя которые в заданных пределах, мы управляем объектом.
4. Наличие ограничений.
Большинство реальных задач содержат ограничения. Наличие ограничений существенно влияет на получение решения оптимизационной задачи. Некоторые задачи можно рассматривать как задачи безусловной оптимизации. В таких задачах ограничения очень широкие и не влияют на результат решения задачи.
5. По особенностям целевой функции.
Целевая функция может быть задана математически различными способами:
· Аналитический способ F = (u1, u2, …, um). Имеется некое аналитическое выражение, при подстановке в которое значений аргументов может быть определено значение функции.
· Алгоритм, т.е. последовательность вычислений, в результате выполнения которых определяется значение целевой функции при заданных значениях ее аргументов (оптимизирующих факторов).
Целевая функция может быть линейной или нелинейной относительно оптимизирующих факторов. В задачах линейного программирования, например, целевая функция линейная. Существует много задач с нелинейно-заданной функцией.
Итак, выбор математического метода решения оптимизационных задач зависит от свойств поставленной задачи. К настоящему времени существует достаточно много математических методов решения оптимизационных задач. По особенностям их реализации методы можно объединить в три группы:
1. Аналитические.
2. Поисковые.
3. Экспериментальные.


