Эффект Холла
Ранее были рассмотрены кинетические явления в полупроводниках (перенос свободных носителей заряда) под действием электрического поля, а также при наличии градиента концентрации (градиента температуры).
Гальваномагнитными называют кинетические явления, которые возникают при одновременном действии электрического и магнитного полей.
Если полупроводник (или проводник), вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное к направлению тока, то в материале возникает поперечное электрическое поле, перпендикулярное к току и магнитному полю. Это явление получило название эффекта Холла, а возникающая поперечная э.д.с. – э.д.с. Холла.
Допустим, что по полупроводнику в виде прямоугольной пластины (рис. 4.17) протекает ток с плотностью
. (4.17)
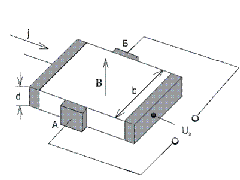
Рис. 4.17. Образец для измерения э.д.с. Холла
Если полупроводник однородный, то его эквипотенциальные поверхности располагаются перпендикулярно к вектору электрического поля e, следовательно, и к вектору плотности тока j. С учетом сказанного разность потенциалов между точками А и Б будет равной нулю, так как точки лежат в плоскости, перпендикулярной к вектору j. При помещении такого полупроводника в магнитное поле напряженностью В, на носитель заряда, дрейфующий со скоростью nдр, будет действовать сила Лоренца
. (4.18)
Если скорость носителей заряда определяется внешним электрическим полем, то направление силы Лоренца не зависит от знака заряда, а определяется только взаимным направлением векторов e и В, т. е. и электроны, и дырки под действием силы Лоренца отклоняются в одну и ту же сторону. При этом в слабом магнитном поле траектория движения носителей изменяется слабо, а в сильном поле наблюдается значительное искривление траектории.
Для выбранных на рис. 4.18 направлений e и В сила Лоренца действует вверх. Под действием этой силы носители заряда в полупроводнике будут смещаться к верхней поверхности образца. На нижней поверхности полупроводника возникает дефицит носителей заряда и появляется электрическое поле напряженностью eх, перпендикулярное к направлению внешнего поля e и магнитного поля В. Это явление возникновения поперечной э.д.с. в полупроводнике с текущим током под действием магнитного поля и называют эффектом Холла. Напряженность поля eх возрастает до тех пор, пока сила, обусловленная этим полем, не скомпенсирует силу Лоренца:
. (4.19)
Если ширину образца принять равной b, то холловская разность потенциалов
. (4.20)
Воспользовавшись выражением (4.17), можно записать
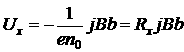. (4.21)
Рис. 4.18. Отклонение носителей заряда под действием магнитного поля в электронном полупроводнике (а) и в дырочном полупроводнике (б)
Величину Rx принято называть коэффициентом (постоянной) Холла. Для электронных полупроводников
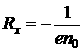, (4.22)
а для дырочных полупроводников
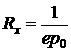. (4.23)
Коэффициент Холла обратно пропорционален концентрации основных носителей заряда, а знак его совпадает со знаком этих носителей. Обратно пропорциональная зависимость э.д.с. Холла от концентрации свободных носителей заряда объясняется тем, что при определенной величине тока носители перемещаются тем быстрее и отклоняются магнитным полем тем сильнее, чем меньше их концентрация.
Рассмотренные выше зависимости не учитывают распределения носителей заряда в объеме полупроводника по скоростям. Для учета механизмов рассеяния носителей заряда в полупроводнике вводится холл-фактор r. Тогда для электронного полупроводника коэффициент Холла будет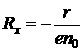 
. При рассеянии на тепловых колебаниях кристаллической решетки r=3p/8, при рассеянии на ионах примеси r=315p/512»1,93. Поскольку рассеяние носителей заряда зависит от температуры, то при определении коэффициента Холла при низких температурах необходимо полагать r=1,93. Для температур, при которых имеет место рассеяние на тепловых колебаниях кристаллической решетки, r=3p/8. Если в процессе рассеяния одновременно участвуют колебания решетки и ионы примеси, r имеет более сложное выражение.
Произведение |Rx|s имеет размерность подвижности и называется холловской подвижностью носителей заряда mх. В то же время удельная электропроводность полупроводника, определяемая дрейфовой подвижностью, находится как s=enmдр. Тогда mx=rmдр, то есть холловская подвижность пропорциональна дрейфовой подвижности. Для металлов и вырожденных полупроводников коэффициент Холла не зависит от механизма рассеяния, поэтому mx=mдр.
Для полупроводников с двумя типами носителей, концентрации и подвижности которых соответственно равны n0, mn и р0, mр, коэффициент Холла
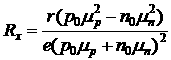. (4.24)
Для собственного полупроводника n0=p0=ni
, (4.25)
где b=mn/mp. Так как обычно b>1, то в собственных полупроводниках Rx<0. Согласно (4.24) инверсия знака Rx может наблюдаться в биполярных полупроводниках.
Поскольку подвижность и концентрация носителей заряда являются функциями температуры, то Rx также зависит от температуры. Измерения зависимости коэффициента Холла от температуры имеют особую ценность. Они позволяют установить температурную зависимость концентрации носителей заряда, а в совокупности с измерениями удельной электропроводности – температурную зависимость подвижности.
По температурной зависимости концентрации или коэффициента Холла в области слабой ионизации примеси можно определить энергию ионизации примеси (DEа, DEД), а в области собственной электропроводности – ширину запрещенной зоны (DЕ0). На рис. 4.19 приведены зависимости концентрации носителей заряда (рис. 4.19, а) и коэффициента Холла (рис. 4.19, б, в) в соответствующих координатах, когда эти зависимости имеют вид прямых линий. Кривая на рис. 4.19, б соответствует полупроводнику n-типа, а на рис. 4.19, в – полупроводнику p-типа. В области примесной проводимости Rx в таком полупроводнике положителен, а в области собственной проводимости – отрицателен [согласно (4.25)]. При переходе к собственной проводимости Rx меняет знак, переходя через нуль, а зависимость lnRx при этом терпит разрыв.
Ранее было указано, что холловское напряжение прямо пропорционально индукции магнитного поля для полей не слишком высокой напряженности. Расчет показал, что критерием слабого поля и, следовательно, применимости полученных выше соотношений для э.д.с. Холла и коэффициента Холла является условие:
, (4.26)
где j – угол Холла, m – подвижность.
|
|
|
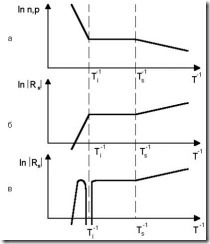
Рис. 4.19. Зависимость концентрации носителей заряда (а) и коэффициента Холла для полупроводника n-типа (б) и полупроводника p-типа (в)
Если в магнитных полях высокой напряженности угол Холла, то есть угол, на который отклоняются свободные носители заряда, будет близок к 2p, то за время свободного пробега носители будут не просто отклоняться от направления своего первоначального движения, а «закручиваться» вокруг силовых линий магнитного поля. Установлено, что слабыми могут считаться магнитные поля с индукцией В: для германия – менее 16 Тл, для кремния – менее 40 Тл, для антимонида индия – менее 0,8 Тл.
Необходимо отметить, что величина э.д.с. Холла в полупроводниках может на порядки величины превышать значение э.д.с. Холла в проводниковых материалах.
Эффект Холла является, таким образом, мощным экспериментальным средством изучения фундаментальных параметров полупроводников: концентрации и знака заряда носителей, а также их подвижности, энергии ионизации примеси и ширины запрещенной зоны. Кроме того, эффект Холла применяют в магнитометрах, измерителях малых перемещений и давлений, бесконтактных переключателях и других устройствах.