Машиностроение и механика

Зависимость концентрации свободных носителей заряда в полупроводниках от температуры

Как отмечалось, концентрация свободных носителей заряда в полупроводниках увеличивается под влиянием температуры, электромагнитного, ионизирующего излучений и других внешних факторов. Если температура постоянна и никакие другие внешние факторы на полупроводник не воздействуют, то такое состояние называют термодинамически равновесным. В этом случае скорость генерации свободных носителей заряда равна скорости их рекомбинации. Такие носители заряда получили название равновесных. Их концентрации обозначают через n₀ и p₀ (для электронов и дырок соответственно).

Концентрации свободных равновесных носителей заряда в полупроводнике (электронов в зоне проводимости и дырок в валентной зоне) определяются эффективной плотностью энергетических состояний в разрешенных зонах и их фактическим заполнением [2, 5]. Значение эффективной плотности разрешенных состояний определяется с позиций квантовой механики соотношениями неопределенностей Гейзенберга, а вероятность их заполнения – статистической вероятностной функцией Ферми – Дирака [5].

Теория показывает, что в общем виде концентрация свободных электронов в зоне проводимости полупроводника при любой температуре

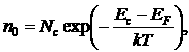(4.1)

а концентрация свободных дырок в валентной зоне

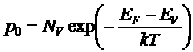, (4.2)

где N_c и N_V – эффективные плотности разрешенных состояний в зоне проводимости и валентной зоне соответственно; E_F – уровень (энергия) Ферми полупроводника (вероятностная характеристика материала), при пересечении уровня Ферми с каким–либо энергетическим уровнем в запрещенной зоне полупроводника вероятность заполнения этого уровня равна 0,5; k – постоянная Больцмана; Т – температура.

Для собственного полупроводника n₀=p₀=n_i. С учетом закона действующих масс

n₀p₀=n_i², (4.3)

концентрация собственных носителей заряда определяется как квадратный корень из произведения (4.1) и (4.2):

. (4.4)

Из (4.1) – (4.3) следует, что концентрация свободных носителей заряда как собственных, обусловленных нарушением ковалентных связей, так и примесных, возникших в результате ионизации атомов примеси, возрастает при увеличении температуры по экспоненциальному закону. Предэкспоненциальные множители N_c и N_v также зависят от температуры, но зависимость эта более слабая – степенная:

. (4.5)

Температурную зависимость концентрации свободных носителей заряда, изображенную на рис. 4.9, рассмотрим на примере полупроводника n-типа. Зависимость в общем виде имеет три участка: 1– примесной проводимости; 2– истощения примеси; 3 – собственной проводимости.

При температуре абсолютного нуля валентная зона полупроводника полностью заполнена, донорные примеси не ионизированы (донорные уровни заняты электронами), зона проводимости пуста. При повышении температуры начинается ионизация донорных атомов и электроны с донорных уровней переходят в зону проводимости (участок 1 рис. 4.9). Чем выше температура, тем больше концентрация свободных электронов в зоне проводимости.

При температуре Т_S все донорные атомы оказываются ионизированными. Повышение температуры от Т_S до T_i на участке 2 рис. 4.9 (участке истощения примеси) не приводит к росту концентрации свободных носителей, поскольку тепловая энергия кТ>DЕ_Д, но еще недостаточна для возбуждения значительной собственной проводимости – нарушения ковалентных связей полупроводника и перехода электронов из валентной зоны в зону проводимости.

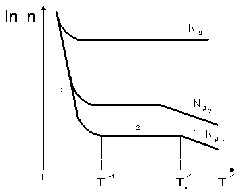
Рис. 4.9. Температурная зависимость концентрации свободных носителей заряда в полупроводнике n-типа: N_Д1Д2Д3

При температуре T_i на участке 3 рис. 4.9 концентрация электронов, приобретающих энергию, достаточную для перехода из валентной зоны в зону проводимости, превышает концентрацию имеющихся в ней электронов, обусловленных ионизацией донорной примеси. При температурах, больших T_i, в полупроводнике наблюдается собственная проводимость.

Из рис. 4.9 видно, что чем выше концентрация примеси, тем выше концентрация электронов на участках 1 и 2 и тем больше значения температур, соответствующих началу истощения примеси и собственной проводимости. Кривая, изображенная на рис. 4.9 для наибольшей концентрации примеси N_Д3, характерна для так называемых вырожденных полупроводников. У таких полупроводников концентрация свободных носителей заряда вплоть до перехода к собственной проводимости не зависит от температуры, а уровень Ферми находится не в запрещенной зоне, а в зоне проводимости.

Установлено, что в области примесной проводимости (на участке 1 рис. 4.9) от температуры абсолютного нуля до T_S температурная зависимость концентрации свободных электронов имеет следующий вид:

, (4.6)

где N_Д – концентрация донорной примеси; DЕ_Д=Е_с - Е_Д – энергия ионизации донорной примеси; .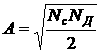

Логарифмируя (4.6), получаем

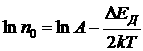. (4.7)

Выражение (4.7) является уравнением прямой с отрицательным угловым коэффициентом, пропорциональным DЕ_Д.

На участке 3 при температурах, больших T_i (рис. 4.9), в области собственной проводимости справедливо соотношение (4.4). Если обозначить , после логарифмирования (4.4) получим

. (4.8)

Выражение (4.8) так же, как (4.7), является уравнением прямой с отрицательным угловым коэффициентом. Тангенс угла наклона прямой пропорционален ширине запрещенной зоны полупроводника DЕ₀. Температурная зависимость концентрации свободных носителей заряда в полупроводниках, построенная в координатах , наглядно показывает характер физических процессов, происходящих при изменении температуры, и позволяет рассчитать параметры полупроводникового материала: энергию ионизации донорной примеси DЕ_Д и энергию, необходимую для разрыва ковалентных связей, – ширину запрещенной зоны DЕ₀.

Отметим, что температурная зависимость концентрации свободных носителей заряда – дырок для полупроводника р-типа выглядит аналогично изображенной на рис. 4.9. Интерпретация зависимости на участке примесной проводимости проводится на основе представлений о захвате акцепторными атомами электронов из валентной зоны и об образовании в ней свободных дырок.

Экспоненциальный закон изменения концентрации свободных носителей заряда при изменении температуры обусловливает принципиальное различие между температурной зависимостью проводимости полупроводников и металлов (рис. 4.1). У последних концентрация свободных носителей от температуры практически не зависит.

<< Prev - Next >>