Машиностроение и механика

Article Index
Полупроводниковые материалы
Энергетические зоны и электрические свойства твердых тел
Собственные и примесные полупроводники
Зависимость концентрации свободных носителей заряда в полупроводниках от температуры
Температурная зависимость проводимости полупроводников
Оптические и фотоэлектрические явления в полупроводниках
Термоэлектрические явления
Эффект Холла
All Pages

ПОЛУПРОВОДНИКОВЫЕ МАТЕРИАЛЫ

Общие свойства и классификация полупроводников

Полупроводники по удельному сопротивлению, которое при комнатной температуре составляет 10^-6–10⁹ Ом×м, занимают промежуточное положение между проводниками и диэлектриками. Они обладают совокупностью физических свойств, которые выделяют их среди других материалов.

В отличие от проводников электропроводность полупроводников увеличивается с ростом температуры (рис. 4.1). Для полупроводников характерна зависимость значения удельной проводимости от вида и количества содержащихся в них примесей. Например, при введении в чистый кремний 0,001 % фосфора его удельная проводимость увеличивается в 10⁵ раз.

0

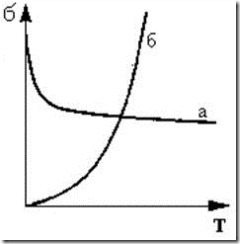
Рис. 4.1. Зависимость удельной проводимости от температуры для металлов (а) и полупроводников (б)

Свойства полупроводниковых материалов сильно зависят от внешних факторов – электрического и магнитного полей, электромагнитного и ядерного излучений и др.

По химическому составу полупроводниковые материалы делят на простые вещества (атомные, элементарные полупроводники – германий, кремний, теллур и др.) и химические соединения различных типов. Если входящие в состав соединений вещества обозначить как А и В, то основные типы бинарных соединений представляют следующим образом: A^IIB^VI(Cu₂O, CuS и др.), A^IIIB^V(GaAs, GaP, InP и др.), A^IVB^IV(SiC и др.). Полупроводниковые свойства присущи тройным соединениям CuAlS₂, CuSbS₂, CuFeS₂, ZnSiAs₂, PbBiSe₂ и твердым растворам GeSi, GaAs_1-xP_x, In_xAl_1-xSb и др. К твердым органическим полупроводникам относятся фталоцианин, антрацен, нафталин и др.

Основным типом химической связи между атомами в элементарных полупроводниках является ковалентная, в химических соединениях – смешанная ионно-ковалентная. Наиболее распространенными типами кристаллической структуры являются структура типа алмаза (ГЦК с базисом) для простых веществ; сфалерита и вюрцита – для химических соединений. По структуре полупроводниковые материалы могут быть монокристаллическими, поликристаллическими и неупорядоченными (стеклообразными).

Уникальные свойства полупроводниковых материалов обусловили широкое техническое применение их для изготовления самых различных приборов – полупроводниковых диодов, транзисторов, тиристоров, фотодиодов, фототранзисторов, светодиодов, полупроводниковых лазеров, а также датчиков давлений, магнитных полей, температур, излучений и др. Использование полупроводников вызвало коренные преобразования в радиотехнике, кибернетике, автоматике, телемеханике. Полупроводниковая электроника открыла новые пути микроминиатюризации различного электронного оборудования.

Энергетические зоны и электрические свойства твердых тел

Понимание физических явлений, происходящих в полупроводниках, невозможно без знания положений зонной теории твердого тела, основанных на представлениях квантовой механики.

Электрон в изолированном атоме может находиться лишь на строго определенных дискретных энергетических уровнях, которые разделены интервалами запрещенных энергий. Дискретность значений энергии электронов в изолированном атоме подтверждается характером спектров поглощения и излучения разреженных газов, т.е. определенными спектральными линиями, наличие которых объясняется переходом электрона с одного уровня на другой, при котором излучается или поглощается свет определенной частоты, соответствующей разности энергий этих уровней.

При образовании кристалла благодаря сближению N одинаковых атомов на расстояния, близкие к расстоянию между атомами в кристаллической решетке а, начинает проявляться взаимодействие атомов между собой. В этом случае принцип Паули распространяется на всю совокупность атомов как на единую систему, и в результате такого взаимодействия эквивалентные уровни электронов изолированных атомов образуют не энергетические уровни Е₁–Е₃, на каждом из которых находится в N раз больше электронов, а энергетические зоны, состоящие из N уровней (рис. 4.2). Так как в кристалле объемом 1 м³ имеется примерно 10²⁸атомов, а ширина энергетической зоны порядка 1 эВ, расстояние между энергетическими уровнями в зоне составляет около 10^-28 эВ.

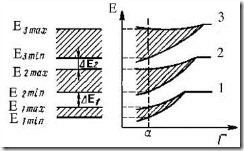
Рис. 4.2. Энергетические зоны при сближении атомов

Для реально возможных микроскопических объемов кристалла расстояние между энергетическими уровнями не превышает 10^-17 эВ. В то же время при комнатной температуре энергия электронов порядка 0,03 эВ. Поэтому электроны могут свободно переходить с одного уровня на другой внутри зоны; можно считать, что энергетические зоны являются квазинепрерывными.

Энергетические зоны, подобно энергетическим уровням электрона в изолированном атоме, в общем случае разделены интервалами запрещенных энергий DЕ_i, которые называют запрещенными зонами.

Электроны в изолированном атоме стремятся занять уровни с минимальной энергией; верхние энергетические уровни остаются свободными. В соответствии с этим не все энергетические зоны твердого тела заняты электронами. Самую верхнюю из заполненных зон называют валентной зоной, а самую нижнюю из свободных зон – зоной проводимости.

Так как движение электрона во внешнем электрическом поле связано с изменением его скорости и энергии, то на энергетической схеме такое движение соответствует перемещению электрона по близлежащим уровням разрешенной зоны. Это означает, что принимать участие в электропроводности могут только те электроны твердого тела, которые расположены в зонах, не полностью заполненных электронами.

У атомов металлов (за исключением щелочно-земельных элементов) на верхнем занятом электронами уровне электронов меньше, чем возможных состояний. Например, у атома Na электроны по уровням (состояниям) распределены следующим образом: 1s²2s²2p⁶3s. На уровне 3s находится один электрон вместо двух возможных. Валентная зона твердого тела, возникающая в результате расщепления уровня 3s, также оказывается не полностью заполненной.

У элементов II группы таблицы Д.И. Менделеева расщепление соответствующих энергетических уровней происходит таким образом, что полностью заполненная валентная зона и полностью свободная зона проводимости перекрываются, образуя одну общую зону, в которой энергетических состояний больше, чем имеющихся электронов. Электроны таких зон могут принимать участие в электропроводности. Этим и объясняется высокая проводимость элементов этой группы.

У полупроводников и диэлектриков между валентной зоной и зоной проводимости имеется запрещенная зона. При температуре абсолютного нуля и в отсутствие внешнего воздействия их валентная зона полностью заполнена, а зона проводимости свободна от электронов. С этой точки зрения различие между диэлектриком и полупроводником чисто количественное. К полупроводникам условно относят вещества с шириной запрещенной зоны DЕ₀=0,05 – 3 эВ, а к диэлектрикам – вещества с DЕ₀> 3 эВ.

Собственные и примесные полупроводники

Собственными называют полупроводники, не содержащие донорных и акцепторных примесей. Зонная диаграмма таких полупроводников представлена на рис. 4.3,а, где Е_с – нижний энергетический уровень зоны проводимости, называемый дном зоны проводимости; Е_v – верхний энергетический уровень валентной зоны, называемый потолком валентной зоны; DЕ₀ – ширина запрещенной зоны.

Практически чаще пользуются энергетической схемой, изображенной на рис. 4.3,б, где представлены лишь потолок валентной зоны и дно зоны проводимости. Стрелкой обозначен энергетический переход электрона из валентной зоны в зону проводимости, который может быть осуществлен за счет энергии тепловых колебаний решетки или энергии внешнего воздействия на полупроводник. С уходом электрона в зону проводимости в валентной зоне полупроводника остается свободным энергетическое состояние, называемое дыркой, а сама валентная зона становится не полностью заполненной.

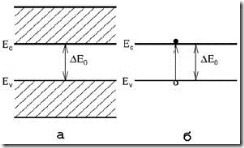
Рис. 4.3. Зонная диаграмма собственного полупроводника

В качестве примера собственного полупроводника рассмотрим монокристалл кремния, являющегося элементом IV группы таблицы Д.И. Менделеева. В кристаллической решетке кремния у каждого атома с каждым из четырех ближайших к нему соседей существует ковалентная связь. Плоская модель кристаллической решетки кремния представлена на рис. 4.4, где имеется изображение символа ковалентной связи, в которой участвуют два электрона. При разрыве ковалентной связи между атомами кремния образуются свободный электрон и незавершенная связь, которой на зонной диаграмме соответствует возможное, но не занятое электроном состояние в валентной зоне – дырка. При отсутствии внешнего электрического поля дырка, как и электрон, будет совершать хаотическое движение в пределах кристалла. Происходит это вследствие того, что электрон соседней ковалентной связи за счет энергии тепловых колебаний решетки может заполнить незавершенную ковалентную связь, в результате чего дырка из положения 1 перейдет в положение 2. По этим же причинам она может перейти в положение 3,4 и т.д. Таким образом, движение дырки осуществляется за счет перемещения электрона, участвующего в ковалентной связи.

Итак, в результате разрыва ковалентной связи образуется пара свободных носителей заряда – электрон в зоне проводимости и дырка в валентной зоне, которые и создают собственную электропроводность полупроводника. Энергия, необходимая для разрыва ковалентной связи, определяется шириной запрещенной зоны полупроводника. Для кремния она составляет 1,12 эВ. Свободные носители заряда при комнатной температуре возникают вследствие флюктуаций тепловых колебаний решетки, так как средней тепловой энергии решетки при комнатной температуре для разрыва ковалентной связи в кремнии недостаточно.

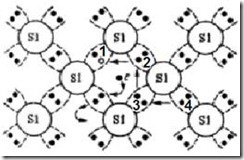
Рис. 4.4. Плоская модель кристаллической решетки собственного полупроводника (кремния)

Примесными называют полупроводники, содержащие донорные и (или) акцепторные примеси.

Если в кремний или германий в качестве примеси ввести элемент V группы таблицы Менделеева, например мышьяк, то атому примеси для завершения ковалентных связей с атомами основного вещества необходимо четыре валентных электрона (рис. 4.5). Пятый валентный электрон атома примеси в ковалентной связи не участвует. Со своим атомом он связан силой кулоновского взаимодействия. Энергия этой связи невелика. Для фосфора, мышьяка, сурьмы она порядка 0,01 эВ в германии и 0,05 эВ в кремнии. Так как при 300 К тепловая энергия kT~0,03 эВ, то очевидно, что при комнатной температуре будет происходить ионизация примесных атомов мышьяка вследствие отрыва пятого валентного электрона, который становится свободным. В германии при 300 К все примесные атомы мышьяка ионизованы. Образовавшиеся при этом положительные ионы примеси принимать участие в электропроводности не могут, так как они локализованы. Находясь в узле кристаллической решетки полупроводника, они являются ее структурными элементами.

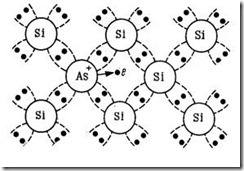
Рис. 4.5. Плоская модель кристаллической решетки полупроводника n-типа (кремния, легированного мышьяком)

Примесь, имеющую валентных электронов больше, чем необходимо для завершения связей между ближайшими атомами основного вещества, и в результате этого способную отдавать электроны, называют донорной, а полупроводник с такой примесью – полупроводником с электронной электропроводностью (или n-типа).

Для того чтобы пятый валентный электрон стал свободным (на энергетической схеме перешел в зону проводимости), необходимо затратить энергию, значительно меньшую, чем для разрыва ковалентной связи. В соответствии с этим энергетический уровень пятого валентного электрона на зонной диаграмме должен располагаться в запрещенной зоне вблизи дна зоны проводимости (рис. 4.6)

Рис. 4.6. Зонная диаграмма полупроводника n-типа

При температуре абсолютного нуля и в отсутствие внешнего воздействия на полупроводник его валентная зона полностью заполнена, зона проводимости пуста, локальные энергетические уровни донорной примеси Е_Д заняты электронами. По мере повышения температуры сначала часть электронов, а затем все электроны с локальных уровней Е_Д перейдут в зону проводимости (переходы 1, рис. 4.6). Наряду с этим будут происходить и переходы 2, обусловленные разрывом ковалентных связей, в результате чего образуется пара свободных носителей заряда: электрон и дырка.

Так как для ионизации донорной примеси требуется энергия значительно меньшая, чем для разрыва ковалентной связи (DЕ_Д), то при температурах, при которых собственная электропроводность проявляется слабо, электропроводность полупроводника определяется в основном электронами, образовавшимися при ионизации донорной примеси. Поэтому электроны в полупроводнике n-типа называют основными носителями заряда, а дырки – неосновными носителями.

Если в полупроводник IV группы таблицы Менделеева ввести в качестве примеси элемент III группы, например алюминий, то все три валентных электрона примесного атома будут участвовать в образовании ковалентных связей. При этом одна из четырех связей с ближайшими атомами основного вещества окажется незавершенной.

Примесь, имеющую валентных электронов меньше, чем это необходимо для завершения связей между ближайшими атомами основного вещества, и вследствие этого способную захватить электроны, называют акцепторной, а полупроводник с такой примесью – полупроводником с дырочной электропроводностью (или p-типа).

Незавершенная связь в результате тепловых колебаний решетки может быть заполнена электроном соседней связи, которая в свою очередь окажется незавершенной (рис. 4.7). Незавершенная связь – дырка за счет тепловых колебаний решетки будет совершать хаотическое движение в пределах кристалла. Атом акцепторной примеси, принявший четвертый электрон для завершения ковалентной связи, становится отрицательным ионом. Такой ион называют ионизированным атомом акцепторной примеси. Принимать участие в электропроводности он не может, так как является структурным элементом кристалла.

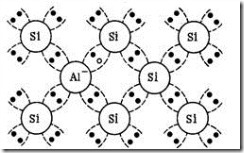
Рис. 4.7. Плоская модель кристаллической решетки полупроводника р-типа (кремния, легированного алюминием)

Для того чтобы образовалась свободная дырка, необходима энергия меньшая, чем для разрыва ковалентной связи (DЕ_а). В германии и кремнии для бора, алюминия, галлия, индия эта энергия составляет 0,01¸0,07 эВ. Значит, локальные энергетические уровни акцепторной примеси Е_а расположены в запрещенной зоне полупроводника вблизи потолка валентной зоны.

При температуре абсолютного нуля и в отсутствие внешнего воздействия на полупроводник акцепторные уровни свободны от электронов. По мере повышения температуры электроны валентной зоны будут заполнять эти локальные уровни при одновременном образовании в валентной зоне соответствующего числа дырок (рис. 4.8, переходы 1). Вместе с тем возможны и переходы 2, при которых образуется пара свободных носителей: электрон–дырка.

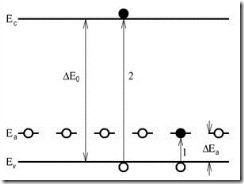
Рис. 4.8. Зонная диаграмма полупроводника р-типа

В полупроводнике р-типа основными носителями заряда являются дырки, неосновными – электроны.

Отметим, что в полупроводниках могут быть примеси, энергетические уровни которых расположены в запрещенной зоне далеко от краев разрешенных зон. Такие уровни называют глубокими. У кремния и германия глубокие уровни возникают при наличии в них примесных атомов золота, меди, кислорода, железа и др.

Рассмотренные зонные модели собственных и примесных полупроводников являются упрощенными, хотя в большинстве случаев они применимы для объяснения физических процессов в полупроводниках и полупроводниковых приборах. Однако есть явления, которые можно объяснить лишь с помощью модели структуры зон, основанной на представлениях квантовой механики с учетом волновых свойств микрочастиц.

Зависимость концентрации свободных носителей заряда в полупроводниках от температуры

Как отмечалось, концентрация свободных носителей заряда в полупроводниках увеличивается под влиянием температуры, электромагнитного, ионизирующего излучений и других внешних факторов. Если температура постоянна и никакие другие внешние факторы на полупроводник не воздействуют, то такое состояние называют термодинамически равновесным. В этом случае скорость генерации свободных носителей заряда равна скорости их рекомбинации. Такие носители заряда получили название равновесных. Их концентрации обозначают через n₀ и p₀ (для электронов и дырок соответственно).

Концентрации свободных равновесных носителей заряда в полупроводнике (электронов в зоне проводимости и дырок в валентной зоне) определяются эффективной плотностью энергетических состояний в разрешенных зонах и их фактическим заполнением [2, 5]. Значение эффективной плотности разрешенных состояний определяется с позиций квантовой механики соотношениями неопределенностей Гейзенберга, а вероятность их заполнения – статистической вероятностной функцией Ферми – Дирака [5].

Теория показывает, что в общем виде концентрация свободных электронов в зоне проводимости полупроводника при любой температуре

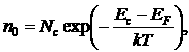(4.1)

а концентрация свободных дырок в валентной зоне

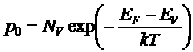, (4.2)

где N_c и N_V – эффективные плотности разрешенных состояний в зоне проводимости и валентной зоне соответственно; E_F – уровень (энергия) Ферми полупроводника (вероятностная характеристика материала), при пересечении уровня Ферми с каким–либо энергетическим уровнем в запрещенной зоне полупроводника вероятность заполнения этого уровня равна 0,5; k – постоянная Больцмана; Т – температура.

Для собственного полупроводника n₀=p₀=n_i. С учетом закона действующих масс

n₀p₀=n_i², (4.3)

концентрация собственных носителей заряда определяется как квадратный корень из произведения (4.1) и (4.2):

. (4.4)

Из (4.1) – (4.3) следует, что концентрация свободных носителей заряда как собственных, обусловленных нарушением ковалентных связей, так и примесных, возникших в результате ионизации атомов примеси, возрастает при увеличении температуры по экспоненциальному закону. Предэкспоненциальные множители N_c и N_v также зависят от температуры, но зависимость эта более слабая – степенная:

. (4.5)

Температурную зависимость концентрации свободных носителей заряда, изображенную на рис. 4.9, рассмотрим на примере полупроводника n-типа. Зависимость в общем виде имеет три участка: 1– примесной проводимости; 2– истощения примеси; 3 – собственной проводимости.

При температуре абсолютного нуля валентная зона полупроводника полностью заполнена, донорные примеси не ионизированы (донорные уровни заняты электронами), зона проводимости пуста. При повышении температуры начинается ионизация донорных атомов и электроны с донорных уровней переходят в зону проводимости (участок 1 рис. 4.9). Чем выше температура, тем больше концентрация свободных электронов в зоне проводимости.

При температуре Т_S все донорные атомы оказываются ионизированными. Повышение температуры от Т_S до T_i на участке 2 рис. 4.9 (участке истощения примеси) не приводит к росту концентрации свободных носителей, поскольку тепловая энергия кТ>DЕ_Д, но еще недостаточна для возбуждения значительной собственной проводимости – нарушения ковалентных связей полупроводника и перехода электронов из валентной зоны в зону проводимости.

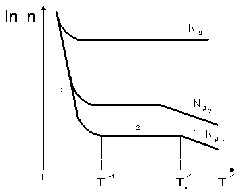
Рис. 4.9. Температурная зависимость концентрации свободных носителей заряда в полупроводнике n-типа: N_Д1Д2Д3

При температуре T_i на участке 3 рис. 4.9 концентрация электронов, приобретающих энергию, достаточную для перехода из валентной зоны в зону проводимости, превышает концентрацию имеющихся в ней электронов, обусловленных ионизацией донорной примеси. При температурах, больших T_i, в полупроводнике наблюдается собственная проводимость.

Из рис. 4.9 видно, что чем выше концентрация примеси, тем выше концентрация электронов на участках 1 и 2 и тем больше значения температур, соответствующих началу истощения примеси и собственной проводимости. Кривая, изображенная на рис. 4.9 для наибольшей концентрации примеси N_Д3, характерна для так называемых вырожденных полупроводников. У таких полупроводников концентрация свободных носителей заряда вплоть до перехода к собственной проводимости не зависит от температуры, а уровень Ферми находится не в запрещенной зоне, а в зоне проводимости.

Установлено, что в области примесной проводимости (на участке 1 рис. 4.9) от температуры абсолютного нуля до T_S температурная зависимость концентрации свободных электронов имеет следующий вид:

, (4.6)

где N_Д – концентрация донорной примеси; DЕ_Д=Е_с - Е_Д – энергия ионизации донорной примеси; .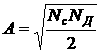

Логарифмируя (4.6), получаем

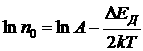. (4.7)

Выражение (4.7) является уравнением прямой с отрицательным угловым коэффициентом, пропорциональным DЕ_Д.

На участке 3 при температурах, больших T_i (рис. 4.9), в области собственной проводимости справедливо соотношение (4.4). Если обозначить , после логарифмирования (4.4) получим

. (4.8)

Выражение (4.8) так же, как (4.7), является уравнением прямой с отрицательным угловым коэффициентом. Тангенс угла наклона прямой пропорционален ширине запрещенной зоны полупроводника DЕ₀. Температурная зависимость концентрации свободных носителей заряда в полупроводниках, построенная в координатах , наглядно показывает характер физических процессов, происходящих при изменении температуры, и позволяет рассчитать параметры полупроводникового материала: энергию ионизации донорной примеси DЕ_Д и энергию, необходимую для разрыва ковалентных связей, – ширину запрещенной зоны DЕ₀.

Отметим, что температурная зависимость концентрации свободных носителей заряда – дырок для полупроводника р-типа выглядит аналогично изображенной на рис. 4.9. Интерпретация зависимости на участке примесной проводимости проводится на основе представлений о захвате акцепторными атомами электронов из валентной зоны и об образовании в ней свободных дырок.

Экспоненциальный закон изменения концентрации свободных носителей заряда при изменении температуры обусловливает принципиальное различие между температурной зависимостью проводимости полупроводников и металлов (рис. 4.1). У последних концентрация свободных носителей от температуры практически не зависит.

Температурная зависимость проводимости полупроводников

Удельная электрическая проводимость любого материала определяется концентрацией и подвижностью свободных носителей заряда, значения которых зависят от температуры.

Подвижность m свободных носителей заряда характеризует их рассеяние и определяется как коэффициент пропорциональности между дрейфовой скоростью v_др и напряженностью электрического поля e: v_др =me.

Рассеяние свободных носителей заряда, т.е. изменение их скорости или направления движения, может происходить из-за наличия в реальных кристаллах полупроводников дефектов структуры (к ним относятся, например, атомы и ионы примеси), тепловых колебаний кристаллической решетки.

Установлено, что при рассеянии носителей заряда только на ионах примеси подвижность

. (4.9)

Увеличение подвижности свободных носителей заряда с повышением температуры объясняется тем, что чем выше температура, тем больше тепловая скорость движения свободного носителя и тем меньше времени он будет находиться в кулоновском поле иона, изменяющего траекторию его движения, а значит, он будет иметь меньшее рассеяние и более высокую подвижность. По мере повышения температуры все более существенное значение приобретает рассеяние на тепловых колебаниях кристаллической решетки, которое при определенной температуре становится преобладающим.

Тепловые колебания кристаллической решетки увеличиваются с ростом температуры, растет и рассеяние носителей, а их подвижность уменьшается. Установлено, что в атомных полупроводниках при рассеянии свободных носителей заряда преимущественно на тепловых колебаниях решетки

. (4.10)

На рис. 4.10 приведены зависимости подвижности свободных носителей заряда в полупроводнике n-типа с разной концентрацией донорной примеси. С повышением температуры при рассеянии на ионах примеси подвижность увеличивается, а затем вследствие все возрастающих колебаний кристаллической решетки и обусловленного ими рассеяния – уменьшается. Величина и положение максимума кривой m(Т^-1) зависят от концентрации примеси. С ее увеличением максимум смещается в область более высоких температур, а вся кривая – вниз по оси ординат. При концентрации примеси, равной N_Д3, соответствующей вырожденному полупроводнику, подвижность уменьшается с ростом температуры аналогично тому, как это происходит в проводниковых материалах (раздел 3.8).

0

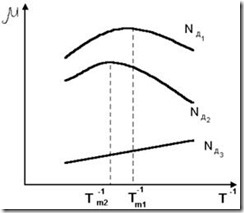
Рис. 4.10. Зависимости подвижности свободных электронов от температуры в полупроводнике n-типа: N_Д1Д2Д3

При очень низких температурах, когда тепловые колебания кристаллической решетки малы, а примесные атомы слабо ионизированы, рассеяние свободных носителей в основном происходит на нейтральных атомах примеси. При таком механизме рассеяния подвижность не зависит от температуры, а определяется концентрацией примеси.

Итак, концентрация свободных носителей заряда в полупроводниках увеличивается с ростом температуры по экспоненциальному закону, а температурная зависимость подвижности имеет в общем виде характер кривой с максимумом и степенной закон изменения.

В общем случае удельная электрическая проводимость s полупроводника, в котором носителями заряда являются свободные электроны с подвижностью m_n и свободные дырки с подвижностью m_р, равна:

, (4.11)

где e – элементарный заряд.

Для собственного полупроводника

. (4.12)

Учитывая, что степенная зависимость слабее экспоненциальной, можно записать:

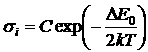. (4.13)

Аналогично для примесного полупроводника n-типа в области примесной проводимости:

, (4.14)

а р-типа:

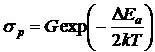. (4.15)

Соотношения (4.14) и (4.15) справедливы лишь до тех пор, пока не наступит полная ионизация примеси. Получив экспериментальную зависимость удельной проводимости от температуры в виде lns(T^-1), можно определить ширину запрещенной зоны полупроводника и энергию ионизации примеси по соотношениям (4.13) – (4.15).

Рассмотрим экспериментальные кривые температурной зависимости удельной электрической проводимости кремния, содержащего различное количество донорной примеси (рис. 4.11).

Повышение удельной проводимости кремния с увеличением температуры в области низких температур обусловлено увеличением концентрации свободных носителей заряда – электронов за счет ионизации донорной примеси. При дальнейшем повышении температуры наступает область истощения примеси – полная ее ионизация. Собственная же электропроводность кремния заметно еще не проявляется.

В условиях истощения примеси концентрация свободных носителей заряда практически от температуры не зависит и температурная зависимость удельной проводимости полупроводника определяется зависимостью подвижности носителей от температуры. Наблюдаемое в этой области уменьшение удельной проводимости кремния с ростом температуры происходит за счет снижения подвижности при рассеянии свободных носителей заряда на тепловых колебаниях кристаллической решетки.

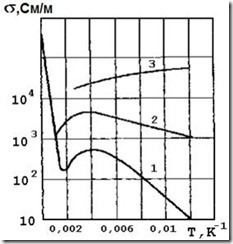
Рис. 4.11. Температурная зависимость удельной электрической проводимости кремния, содержащего различное количество донорной примеси N_Д: 1 – 4,8×10²³; 2 – 2,7×10²⁴; 3 – 4,7×10²⁵ м^-3 [2]

Однако возможен и такой случай, когда область истощения примеси оказывается в интервале температур, где основным механизмом рассеяния является рассеяние на ионах примеси. Тогда удельная проводимость полупроводника с повышением температуры будет увеличиваться: s~T^3/2.

Резкое увеличение удельной проводимости при дальнейшем росте температуры (рис. 4.11) соответствует области собственной электропроводности, в которой концентрация увеличивается экспоненциально [соотношение (4.4)], а подвижность снижается по степенному закону (4.10).

У вырожденного полупроводника (кривая 3 на рис. 4.11) концентрация свободных носителей заряда не зависит от температуры и температурная зависимость проводимости определяется зависимостью их подвижности от температуры (рис. 4.10).

Оптические и фотоэлектрические явления в полупроводниках

Поглощение света. Вследствие отражения и поглощения света полупроводником интенсивность падающего на него монохроматического излучения интенсивностью I₀ уменьшается до некоторой величины I. В соответствии с законом Ламберта – Бугера [2]:

, (4.16)

где R – коэффициент отражения, x – расстояние от поверхности полупроводника вдоль направления луча (в объеме) до данной точки; a – коэффициент поглощения.

Величина a^-1 равна толщине слоя вещества, при прохождении через который интенсивность света уменьшается в e раз (е – основание натурального логарифма).

Поглощение полупроводником энергии электромагнитного излучения может быть связано с различными физическими процессами: нарушением ковалентных связей между атомами материала с переходом электронов из валентной зоны в зону проводимости; ионизацией примесных атомов и возникновением дополнительных свободных электронов или дырок; изменением колебательной энергии атомов решетки; образованием экситонов и др.

Если поглощение света полупроводником обусловлено переходами электронов из валентной зоны в зону проводимости за счет энергии квантов излучения, то поглощение называют собственным; если возникновением свободных носителей за счет ионизации примесных атомов (доноров или акцепторов) – примесным.

У ряда полупроводников за счет поглощения кванта света возможно такое возбуждение электрона валентной зоны, которое не сопровождается его переходом в зону проводимости, а образуется связанная система электрон–дырка, перемещающаяся в пределах кристалла как единое целое. Эту систему называют экситоном. Оптическое поглощение полупроводника, обусловленное взаимодействием излучения с колебательным движением кристаллической решетки, называют решеточным [2, 5]. Независимо от механизма поглощения квантов излучения процесс подчиняется закону сохранения энергии.

Фотопроводимость полупроводников – явление, всегда сопровождающее процесс поглощения энергии электромагнитного излучения. При освещении полупроводника концентрация свободных носителей заряда в нем может возрасти за счет носителей, возбужденных поглощенными квантами света. Такими носителями могут быть как собственные электроны и дырки, так и носители, перешедшие в свободное состояние вследствие ионизации примесных атомов.

Освещение полупроводника светом в течение достаточно длительного времени не приводит к бесконечному росту концентрации избыточных (по сравнению с равновесными) носителей заряда, так как по мере роста концентрации свободных носителей растет вероятность их рекомбинации. Наступает момент, когда рекомбинация уравновешивает процесс генерации свободных носителей и устанавливается равновесное состояние полупроводника с более высокой проводимостью s_равн, чем без освещения (s₀).

0

0

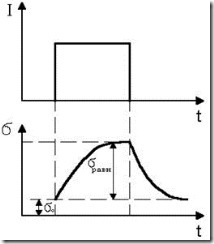
Рис. 4.12. Изменение фотопроводимости полупроводника во времени при освещении его прямоугольным импульсом света

Изложенное иллюстрируется рис. 4.12. Изменение фотопроводимости при освещении полупроводника импульсом прямоугольной формы происходит в соответствии с изменением концентрации свободных носителей заряда.

Спектральная зависимость фотопроводимости соответствует спектру поглощения полупроводника, т.е. зависимости коэффициента поглощения a от длины волны излучения l (рис. 4.13).

0

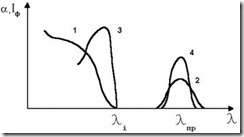
Рис. 4.13. Спектр поглощения полупроводника и спектральное распределение фоточувствительности: 1 – собственное поглощение; 2 – примесное поглощение; 3,4 – фототок

При более длинноволновом излучении, когда энергия квантов света Е_Ф невелика (Е_ф=hn, где h – постоянная Планка, n – частота), при l_пр наступает примесное поглощение и возникает фотопроводимость (фототок) за счет ионизации примесей (кривые 2, 4, рис. 4.13). При меньшей длине волны l_i, т.е. большей энергии квантов света, соизмеримой с шириной запрещенной зоны, полупроводника DЕ₀, возникают собственное (фундаментальное) поглощение и фотопроводимость (фототок) (кривые 1,3, рис. 4.13). Такая длина волны l_i называется краем собственного (фундаментального) поглощения полупроводника. Коротковолновый спад фотопроводимости (кривая 3, рис. 4.13) объясняется высоким коэффициентом поглощения (кривая 1, рис. 4.13), т.е. практически весь свет поглощается в очень тонком поверхностном слое материала.

Как указано выше, фотопроводимость, вызванная генерацией свободных носителей, всегда сопровождается поглощением энергии электромагнитного излучения. В процессе рекомбинации, напротив, энергия выделяется. Выделяющаяся энергия может поглощаться кристаллической решеткой (безызлучательная рекомбинация) либо излучаться в виде кванта света (излучательная рекомбинация). Последнее явление нашло применение в светодиодах, используемых в приборостроении в качестве световых индикаторов.

Термоэлектрические явления

К важнейшим термоэлектрическим явлениям в полупроводниках относятся эффекты Зеебека, Пельтье и Томсона.

Эффект Зеебека (термоэлектрический эффект) состоит в возникновении э.д.с. в электрической цепи, состоящей из последовательно соединенных разнородных материалов (разных металлов или полупроводников или металла и полупроводника), если температуры контактов различны (рис. 4.14).

Термо-э.д.с. имеет три составляющие. Первая составляющая обусловлена диффузией носителей заряда из области полупроводника с более высокой температурой в область с более низкой (рис. 4.15). Градиент концентрации возникает вследствие дополнительной генерации основных или собственных носителей под возникновением повышенной температуры. Таким образом, градиент температуры вызывает создание градиента концентрации носителей заряда с их последующей диффузией к менее нагретому контакту. Вследствие указанных процессов «холодный» контакт приобретает знак основных носителей заряда, а «горячий» – знак соответствующих ионизированных донорных или акцепторных атомов примеси. Ионы являются элементами кристаллической решетки полупроводника и создают неподвижный

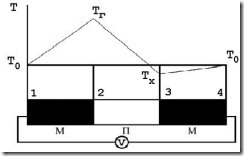
объемный заряд: положительный в полупроводнике n-типа или отрицательный в полупроводнике р-типа.

Рис. 4.14. Схема распределения температур в термоэлементе

Таким образом, диффузионная составляющая термо-э.д.с. возникает из–за нарушения (вследствие диффузии) электрической нейтральности областей полупроводника с разной температурой.

Вторая составляющая термо-э.д.с. – это следствие температурной зависимости контактной разности потенциалов. Если оба спая (рис. 4.14) имеют одну и ту же температуру, то контактные разности потенциалов на этих спаях равны, направлены в противоположные стороны и не дают результирующей термо-э.д.с. Если же температура сплава различна, то величина контактной разности потенциалов будет также различна. Поэтому в цепи термоэлемента появляется вторая составляющая термо-э.д.с. с той же полярностью, что и диффузионная.

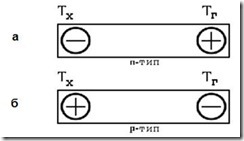
Рис. 4.15. Объемные заряды в полупроводнике n-типа (а) и р-типа (б) при наличии разности температур

Третья составляющая термо-э.д.с. возникает в термоэлементе вследствие увлечения электронов (дырок) фононами, т.е. квантами тепловой энергии колебаний кристаллической решетки. Если в полупроводнике существует градиент температуры, то будет существовать направленное движение фононов от горячего спая к холодному. В результате столкновения фононов с носителями заряда фононы увлекают за собой в n-полупроводнике электроны, а в р-полупроводнике – дырки. Этот эффект может оказаться преобладающим при низких температурах.

Результирующая термо-э.д.с., состоящая их трех рассмотренных составляющих, зависит от температуры горячего (Т_г) и холодного (Т_х) спаев, от электрофизических свойств материалов.

Эффект Пельтье состоит в охлаждении или нагревании контакта двух материалов при протекании через него постоянного тока (рис. 4.16).

Если напряженность внешнего электрического поля e направлена так, как изображено на рис. 4.16, то перенос носителей тока через контакт (электрический ток) будет связан с переходом электронов из полупроводника в металл. Однако энергия электронов в зоне проводимости полупроводника больше, чем у электронов проводимости в металле. Поэтому электроны, переходя из полупроводника в металл, избыток энергии передадут кристаллической решетке в области контакта. В результате этого перенос электронов из полупроводника в металл будет сопровождаться выделением тепла на контакте и его нагревом.

При противоположном направлении напряженности внешнего электрического поля прохождение электрического тока будет связано с переходом электронов из металла в полупроводник, т.е. с уровней с меньшей энергией на уровни с большей энергией. Энергию, необходимую для этого, электроны получают от кристаллической решетки в области контакта, что приводит к его охлаждению.

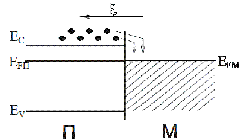
Рис. 4.16. Схема контакта электронного полупроводника с металлом,
поясняющая эффект Пельтье [2]

Эффект Томсона состоит в выделении или поглощении тепла, дополнительно к теплу Джоуля – Ленца, при протекании постоянного тока по однородному полупроводнику, в котором имеется градиент температуры.

Эффекты Зеебека и Пельтье наблюдаются в металлах и полупроводниках. В полупроводниках соответствующие величины, например термо-э.д.с., обычно на несколько порядков превышают таковые в металлах. Поэтому эффекты Зеебека и Пельтье в полупроводниках нашли большое практическое применение. В частности, эффект Зеебека используется для создания источников питания. К.п.д. полупроводниковых термогенераторов достигает 15–20 %. Термоэлектрические явления используются также в технике измерения электрофизических параметров полупроводников для определения типа их проводимости (рис. 4.15).

Термоэлектрический эффект Зеебека применяется для измерения температуры (термопары) и при других измерениях, которые могут быть сведены к измерению температуры.

Эффект Пельтье используется при создании компактных холодильных установок.

Эффект Холла

Ранее были рассмотрены кинетические явления в полупроводниках (перенос свободных носителей заряда) под действием электрического поля, а также при наличии градиента концентрации (градиента температуры).

Гальваномагнитными называют кинетические явления, которые возникают при одновременном действии электрического и магнитного полей.

Если полупроводник (или проводник), вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное к направлению тока, то в материале возникает поперечное электрическое поле, перпендикулярное к току и магнитному полю. Это явление получило название эффекта Холла, а возникающая поперечная э.д.с. – э.д.с. Холла.

Допустим, что по полупроводнику в виде прямоугольной пластины (рис. 4.17) протекает ток с плотностью

. (4.17)

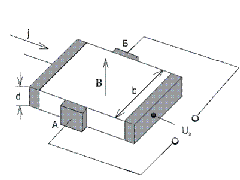
Рис. 4.17. Образец для измерения э.д.с. Холла

Если полупроводник однородный, то его эквипотенциальные поверхности располагаются перпендикулярно к вектору электрического поля e, следовательно, и к вектору плотности тока j. С учетом сказанного разность потенциалов между точками А и Б будет равной нулю, так как точки лежат в плоскости, перпендикулярной к вектору j. При помещении такого полупроводника в магнитное поле напряженностью В, на носитель заряда, дрейфующий со скоростью n_др, будет действовать сила Лоренца

. (4.18)

Если скорость носителей заряда определяется внешним электрическим полем, то направление силы Лоренца не зависит от знака заряда, а определяется только взаимным направлением векторов e и В, т. е. и электроны, и дырки под действием силы Лоренца отклоняются в одну и ту же сторону. При этом в слабом магнитном поле траектория движения носителей изменяется слабо, а в сильном поле наблюдается значительное искривление траектории.

Для выбранных на рис. 4.18 направлений e и В сила Лоренца действует вверх. Под действием этой силы носители заряда в полупроводнике будут смещаться к верхней поверхности образца. На нижней поверхности полупроводника возникает дефицит носителей заряда и появляется электрическое поле напряженностью e_х, перпендикулярное к направлению внешнего поля e и магнитного поля В. Это явление возникновения поперечной э.д.с. в полупроводнике с текущим током под действием магнитного поля и называют эффектом Холла. Напряженность поля e_х возрастает до тех пор, пока сила, обусловленная этим полем, не скомпенсирует силу Лоренца:

. (4.19)

Если ширину образца принять равной b, то холловская разность потенциалов

. (4.20)

Воспользовавшись выражением (4.17), можно записать

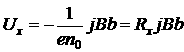. (4.21)

Рис. 4.18. Отклонение носителей заряда под действием магнитного поля в электронном полупроводнике (а) и в дырочном полупроводнике (б)

Величину R_x принято называть коэффициентом (постоянной) Холла. Для электронных полупроводников

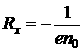, (4.22)

а для дырочных полупроводников

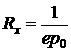. (4.23)

Коэффициент Холла обратно пропорционален концентрации основных носителей заряда, а знак его совпадает со знаком этих носителей. Обратно пропорциональная зависимость э.д.с. Холла от концентрации свободных носителей заряда объясняется тем, что при определенной величине тока носители перемещаются тем быстрее и отклоняются магнитным полем тем сильнее, чем меньше их концентрация.

Рассмотренные выше зависимости не учитывают распределения носителей заряда в объеме полупроводника по скоростям. Для учета механизмов рассеяния носителей заряда в полупроводнике вводится холл-фактор r. Тогда для электронного полупроводника коэффициент Холла будет 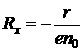. При рассеянии на тепловых колебаниях кристаллической решетки r=3p/8, при рассеянии на ионах примеси r=315p/512»1,93. Поскольку рассеяние носителей заряда зависит от температуры, то при определении коэффициента Холла при низких температурах необходимо полагать r=1,93. Для температур, при которых имеет место рассеяние на тепловых колебаниях кристаллической решетки, r=3p/8. Если в процессе рассеяния одновременно участвуют колебания решетки и ионы примеси, r имеет более сложное выражение.

Произведение |R_x|s имеет размерность подвижности и называется холловской подвижностью носителей заряда m_х. В то же время удельная электропроводность полупроводника, определяемая дрейфовой подвижностью, находится как s=enm_др. Тогда m_x=rm_др, то есть холловская подвижность пропорциональна дрейфовой подвижности. Для металлов и вырожденных полупроводников коэффициент Холла не зависит от механизма рассеяния, поэтому m_x=m_др.

Для полупроводников с двумя типами носителей, концентрации и подвижности которых соответственно равны n₀, m_n и р₀, m_р, коэффициент Холла

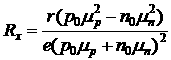. (4.24)

Для собственного полупроводника n₀=p₀=n_i

, (4.25)

где b=m_n/m_p. Так как обычно b>1, то в собственных полупроводниках R_x<0. Согласно (4.24) инверсия знака R_x может наблюдаться в биполярных полупроводниках.

Поскольку подвижность и концентрация носителей заряда являются функциями температуры, то R_x также зависит от температуры. Измерения зависимости коэффициента Холла от температуры имеют особую ценность. Они позволяют установить температурную зависимость концентрации носителей заряда, а в совокупности с измерениями удельной электропроводности – температурную зависимость подвижности.

По температурной зависимости концентрации или коэффициента Холла в области слабой ионизации примеси можно определить энергию ионизации примеси (DE_а, DE_Д), а в области собственной электропроводности – ширину запрещенной зоны (DЕ₀). На рис. 4.19 приведены зависимости концентрации носителей заряда (рис. 4.19, а) и коэффициента Холла (рис. 4.19, б, в) в соответствующих координатах, когда эти зависимости имеют вид прямых линий. Кривая на рис. 4.19, б соответствует полупроводнику n-типа, а на рис. 4.19, в – полупроводнику p-типа. В области примесной проводимости R_x в таком полупроводнике положителен, а в области собственной проводимости – отрицателен [согласно (4.25)]. При переходе к собственной проводимости R_x меняет знак, переходя через нуль, а зависимость lnR_x при этом терпит разрыв.

Ранее было указано, что холловское напряжение прямо пропорционально индукции магнитного поля для полей не слишком высокой напряженности. Расчет показал, что критерием слабого поля и, следовательно, применимости полученных выше соотношений для э.д.с. Холла и коэффициента Холла является условие:

, (4.26)

где j – угол Холла, m – подвижность.

0

0

0

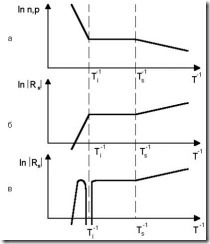
Рис. 4.19. Зависимость концентрации носителей заряда (а) и коэффициента Холла для полупроводника n-типа (б) и полупроводника p-типа (в)

Если в магнитных полях высокой напряженности угол Холла, то есть угол, на который отклоняются свободные носители заряда, будет близок к 2p, то за время свободного пробега носители будут не просто отклоняться от направления своего первоначального движения, а «закручиваться» вокруг силовых линий магнитного поля. Установлено, что слабыми могут считаться магнитные поля с индукцией В: для германия – менее 16 Тл, для кремния – менее 40 Тл, для антимонида индия – менее 0,8 Тл.

Необходимо отметить, что величина э.д.с. Холла в полупроводниках может на порядки величины превышать значение э.д.с. Холла в проводниковых материалах.

Эффект Холла является, таким образом, мощным экспериментальным средством изучения фундаментальных параметров полупроводников: концентрации и знака заряда носителей, а также их подвижности, энергии ионизации примеси и ширины запрещенной зоны. Кроме того, эффект Холла применяют в магнитометрах, измерителях малых перемещений и давлений, бесконтактных переключателях и других устройствах.