Динамические режимы работы качающихся конвейеров
Рассмотрим процесс перемещения частицы груза, находящейся внутри трубы (желоба) качающегося конвейера.
При колебательном движении наклонной плоскости (рис. 6.5) под углом α с ускорением jж, направленном под углом β, частица груза, лежащая на этой плоскости, будет перемещаться вдоль данной плоскости [2].
При этом нормальное давление N частицы груза на плоскость (дно трубы или желоба)
N = mg cos α + mjy, (6.11)
где m – масса частицы груза;
jy – составляющая ускорения jж по оси Y;
jy = – jж sin β = – aω2sinφ sinβ. (6.12)
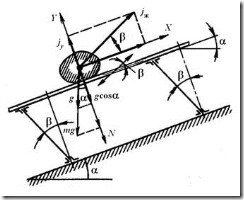
Рис. 6.5. Схема к расчету силы давления груза на желоб
Сила давления груза на плоскость:
N = m (g cosα – aω2sinφ sinβ), (6.13)
где а – амплитуда колебаний плоскости;
ω – угловая скорость возбудителя колебаний;
φ = ωt – фазовый угол колебаний (t – время).
При g cosα > aω2sinφ sinβ сила давления груза на плоскость направлена вниз и является положительной (груз находится на дне желоба).
При g cosα < aω2sinφ sinβ сила давления направлена вверх, и груз стремится оторваться от плоскости. Угол φ изменяется от 0 до 360°, тогда sinφ = 1 при φ = π/2 = 90°.
Коэффициент режима работы качающегося (колебательного) конвейера
![]() . (6.14)
. (6.14)
Для горизонтального конвейера cos α = cos 0° = 1 поэтому
![]() . (6.15)
. (6.15)
Коэффициент Г характеризует динамический режим работы качающегося конвейера и характер движения частиц груза:
при Г < 1 груз лежит на колеблющейся плоскости и перемещается не отрываясь от нее (режим инерционных конвейеров);
при Г > 1 груз отрывается от колеблющейся плоскости и перемещается микробросками (режим вибрационных конвейеров) (рис. 6.6);
при Г = 1 имеют место граничные условия (рис. 6.7).
При выполнении условия 1 < Г ≤ 3,3 движение частицы груза является оптимальным и состоит из нескольких этапов, выполняемых в различные промежутки времени одного периода колебаний плоскости.
Наиболее эффективным является движение частиц груза без скольжения, перемешивания, обратного движения, препятствующих рациональному перемещению.
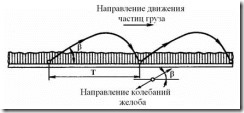
Рис. 6.6. Схема движения частиц груза на вибрационном конвейере

Рис. 6.7. Диаграмма движения частиц груза на вибрационном конвейере
Наиболее рациональными режимами работы конвейера считаются такие, при которых движение частиц происходит при непрерывном подбрасывании и время их микрополета tп составляет tп = ρТ (ρ – любое целое число).
Движение с непрерывным подбрасыванием частиц груза происходит при значении коэффициента Г, определяемом по формуле
![]() . (6.16)
. (6.16)
При ρ = 1 время tп равно одному полному периоду колебания конвейера, а коэффициент режима Г = 3,3; при ρ = 2 tп = 2Т, а коэффициент Г = 6,36 (рис. 6.7).
В результате исследований динамических режимов работы качающихся конвейеров установлено, что при ρ > 1 и Г > 3,3 имеются определенные зоны снижения скорости перемещения груза (не происходит пропорционального увеличения скорости). При этом конвейер работает со значительными ускорениями, обусловливающими большие динамические нагрузки на привод, подшипники и другие элементы. Следовательно, для вибрационного конвейера коэффициент режима работы должен находиться в теоретических пределах 1 < Г ≤ 3,3.


