Электро- и теплопроводность металлов и сплавов
Электропроводность металлов
Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных свободных валентных электронов. К электронному газу применялись представления и законы обычных газов. Это привело к выводу законов Ома и Джоуля – Ленца, позволило описать и объяснить ранее обнаруженные экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах.
Однако исчерпывающее объяснение явлений электропроводности оказалось возможным на основе квантовой механики. В соответствии с квантово–механическими представлениями причиной наличия электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки (как в классической теории Друде), а рассеяние их на дефектах решетки, вызывающих нарушение периодичности потенциала. Идеально правильная, бездефектная неподвижная решетка не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением.
Подвижность и длина свободного пробега электронов в твердом теле зависят от структуры материала. Чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления r. Примеси, искажая решетку, приводят к увеличению r. С позиций квантовой механики рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины волны электрона; нарушения меньших размеров не вызывают заметного рассеяния волн де Бройля. В металлическом проводнике, где длина волны электрона порядка 5 Å, микродефекты создают значительное рассеяние, уменьшающее подвижность электронов и длину свободного пробега, и, следовательно, приводят к росту r.
Так как в металлах концентрация электронного газа n практически не зависит от температуры (Т), то зависимость удельного сопротивления r (и обратной величины удельной электропроводности s) от температуры полностью определяется температурной зависимостью подвижности (m) и пропорциональной ей длины свободного пробега электронов (l).
Вследствие усиления колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т.е. уменьшается среднестатистическая длина свободного пробега l, уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рис. 3.14).

Рис. 3.14. Зависимость удельного сопротивления металлов и сплавов от температуры: 1 – железо; 2 – электротехническая сталь с содержанием 4 % Si; 3 – сплав Fe-Ni-Cr
Удельное сопротивление сплавов
Как указывалось, примеси и нарушения правильной структуры металлов ведут к увеличению их удельного сопротивления.
Значительное возрастание r наблюдается при сплавлении двух металлов в том случае, если они образуют твердый раствор, т.е. создают при отвердевании совместную кристаллизацию, и атомы одного металла входят в кристаллическую решетку другого.
Зависимость удельного сопротивления сплава двух металлов, образующих твердый раствор, от процентного содержания каждого из них представлена на рис. 3.15 (кривая а). Кривая имеет максимум, соответствующий некоторому соотношению содержания компонентов в сплаве; при уменьшении содержания каждого из них r падает, приближаясь к соответствующим значениям r чистых металлов. Обычно наблюдается определенная закономерность и в изменении ТКr (ТК – температурный коэффициент): относительно высокими значениями ТКr обладают чистые металлы, а у сплавов ТКr меньше и даже может приобретать небольшие по абсолютной величине отрицательные значения (рис. 3.15, кривая б). Это объясняется тем, что у сплавов изменение r вызывается не только изменением подвижности носителей заряда, но в некоторых случаях и возрастанием концентрации носителей при повышении температуры.
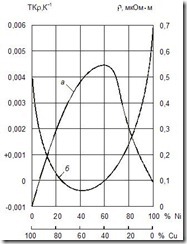
Рис. 3.15. Зависимость r (а) и ТКr (б) сплавов системы Cu-Ni от состава (в процентах по массе)
Теплопроводность
Тепло через металл передается в основном теми же свободными электронами, которые определяют и электропроводность металлов; количество их в единице объема металла весьма велико. Поэтому, как правило, коэффициент теплопроводности h металлов много больше, чем у диэлектриков. Очевидно, что при прочих равных условиях чем больше удельная электрическая проводимость s металла, тем больше его коэффициент теплопроводности h. При повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость s уменьшаются, отношение коэффициента теплопроводности металла к его удельной электрической проводимости h/s должно возрастать. Математически это выражается законом Видемана – Франца – Лорентца:
h/s = L0T, (3.1)
где Т – абсолютная температура, К; L0 – число Лорентца, равное
 . (3.2)
. (3.2)
Подстановка в (3.2) значений постоянной Больцмана k = 1,38×10-23 Дж/К и заряда электрона e = -1,6×10-19 Кл дает L0 = 2,45×10-8 В2/К2.
Закон Видемана – Франца – Лорентца для большинства металлов хорошо подтверждается при температурах, близких к нормальной или несколько повышенных.
Проверим справедливость этого закона для меди при нормальной температуре. Подставляя в формулу (3.1) параметры меди: s = 57×106 См/м и h= 390 Вт/(м×К), получаем (при Т = 293 К) L0 = 2,54×10-8 В2/К2, что весьма близко к теоретическому значению. При нормальной температуре для алюминия L0 = 2,1×10-8, для свинца и олова – 2,5×10-8, для железа – 2,9×10-8 В2/К2.
Однако в области низких температур коэффициент при Т в уравнении (3.1) уже не остается неизменным: так, для меди при охлаждении он проходит через минимум, а при приближении к абсолютному нулю вновь близок к теоретическому значению L0.


