СТАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ
Процессы, протекающие в объектах автоматического управления, зависят от многих факторов. Некоторые из этих факторов известны заранее, другие определяются в процессе работы; однако многие факторы остаются неизвестными и их значения не могут быть предусмотрены и учтены заранее. Химический состав сырья, его физические свойства, распределение материалов в рабочем, пространстве объекта являются случайными факторами, значения которых могут изменяться в известных пределах. В результате случайных событий и случайных значений многих факторов течение процесса и его результаты также являются случайными. Однако, располагая достаточным числом экспериментальных данных о факторах, влияющих на ход процесса и анализируя поведение процесса по его результатам, полученным при различных условиях, модно определить некоторые усредненные характеристики процесса. Для этой цели используют математический аппарат теории вероятности и математической статистики.
Обычно параметры процессов анализируют по структурной схеме статического анализа (см. рис. 1.1).

Рисунок 1.1 – Структурная схема статистического анализа
При статическом анализе сложных объектов не всегда есть возможность регистрировать непрерывные изменения всех исследуемых параметров. Необходимая информация может быть получена путем периодической регистрации исследуемых параметров в моменты времени, разделенные постоянным интервалом, величина которого может колебаться в широких пределах. Практически интервал выбирается из условий St ≤ max τ0j, где τ0j – время спада корреляционной функции переменной.
Промежуток времени Т, в течение которого необходимо проводить наблюдения над объектом определяют по формуле:
![]() ,
,
где δt - интервал регистрации параметра;
λ - параметр, характеризующий количество попаданий исследуемой величины в крайний интервал диапазона ее изменения (значения λ по доверительной вероятности Р приведены в таблице 1.1);
U - частота попадания исследуемой величины в крайний интервал (значения определяют из гистограмм).
Таблица 1.1 – Значения по доверительной вероятности Р
|
Р, % |
94 |
95 |
96 |
97 |
98 |
99 |
|
λ |
3,52 |
3,68 |
3,9 |
4,19 |
4,6 |
5,3 |
Если рассматривать значения реализаций в момент времени tj, получаем случайную величину для данного момента времени, которую можно характеризовать известными количественными признаками – математическим ожиданием М и дисперсией Д:
![]()
откуда среднеквадратичное отклонение
![]()
Математическое ожидание и дисперсия не являются исчерпывающими характеристиками случайных процессов. Для того, чтобы охарактеризовать степень связи между временными сечениями случайного процесса вводят понятие корреляционной функции:
![]()
Для выбора способа решения задачи оптимизации необходимо исследовать частотные характеристики входных и выходных параметров объекта. В качестве частотных характеристик рассматривают нормированные автокорреляционные функция Rxх(τ) и спектральные плотности Sхх(ω). Спектральная плотность определяется как косинус преобразования от Rxх(τ):
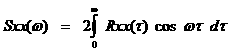 .
.


